皆さま、こんにちは！
今日で９月も終わりです。
少しずつ受験の足音が近づいてきていますね。
１日１日を大切にして、頑張っていきましょう。

さて、前回は「組合せ」の計算を利用して、より複雑な「場合の数」を考えてみました。
（「組合せ」は「選び方」や「コンビネーション」とも言います）
今回は、「組合せ」の計算はこんな問題にも利用できるよ！ということをお伝えします。

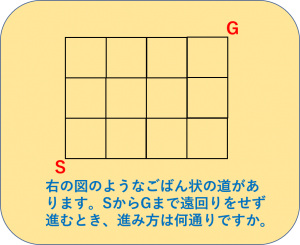
まずは、次のような問題を考えてみてください。

これは「道順」についての問題で、中学受験でよく出題されます。
たいていのテキストに載っている有名問題ですね。
受験ドクターの根本原理では、基礎編の０９６番に出てきます。
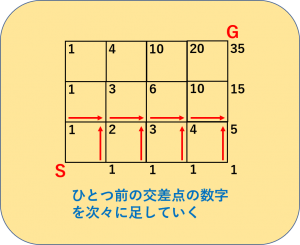
基本的な解き方は、交差点ごとに数えていくものです。
以下のように数字をふって数えていきますね。

すると、答えは３５通りだということがわかります。

なんだ、地道に数えているだけじゃないか！？と思われるかもしれません。
しかし、こういった数え方ができることはとても大切です。
「場合の数」の基本は樹形図だ、ということは、ここまでのブログで何度も強調してきました。
それと同じで、こうやって地道に数える方法は必ず身につけておかないといけません。
その場合でもこの数え方は有効で、実際に、この方法しか知らないという人は大学生でもたくさんいます。
決してバカにするような方法ではないのだ、ということを、ぜひ知っておいてください。
お子様がこの方法でスラスラと「道順」の問題を解いていたら、ぜひ誉めてあげてくださいね。

ところで、この「道順」の問題は、実は「組合せ」の計算を使って解くことができるのです。
これを知っていて、きちんと使いこなせていたら、かなりの「場合の数」上級者です。
さあ、どう使えばいいかわかりますか？
理屈はそこまで複雑ではありません。
説明してみましょう！

まず、スタートからゴールまで、何本の道を通る必要があるのか数えます。
この問題の場合は、7本ですね。
遠回りはしない条件なので、どういう道順でいっても、必ず7本の道を通りますね？
次に、その7本のうちで、縦に移動するのは何本かを数えます。
この場合は、3本ですね。
これも、道順に関わらず、必ず3本は縦に移動しなくてはいけないことを確認してください。
さて、ここまでわかると、この「道順」の問題は次のように言い換えることができます。

スタートからゴールまでの間に、7本の道を通らなくてはいけない。
そのうち、3本は必ず縦に移動する必要がある。
では、7本のうち、縦にする3本を選ぶ方法は何通りですか？

わかりますか？
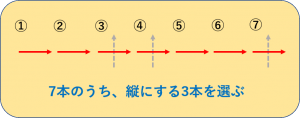
図にすると、次のようなイメージになりますね。

横に7本並んでいる棒を、3本だけ縦にしてみてください、ということです。
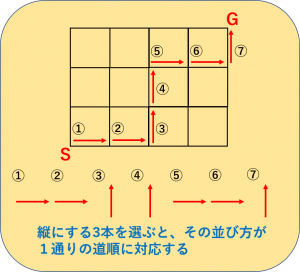
ためしに、適当に3本選んで縦にしてみましょう。
そして、その通りに道をなぞってみてください。

ちゃんと、１通りの「道順」を示しているのがわかるでしょうか？
ということは、「縦にする3本の選び方」の分だけ、「道順」のパターンがあることになります。
そうすると、これが「組合せ」の問題なのだということが、わかってきませんか

横に7本並んでいる棒のうち、縦にする3本を選ぶ方法は何通りか？

こう問われているのと同じことですよね！
ということで、これは７×６×５÷（３×２×１）を計算すればいいということです。
すると、ちゃんと３５通りという答えが出てきますね！

いかかがでしょうか？
「組合せ」の計算の威力は素晴らしいですね！
まさに、抜群のコンビネーション！です。
このように、一見「組合せ」と思えない問題でも、少し考え方を変えると、「組合せ」の問題になるのです。
ポイントは、問題を「言い換える」ということで、これは「場合の数」の重要テクニックです。
次回は、この「言い換え」について、さらに詳しく扱いたいと思います。
お楽しみに！