皆さま、こんにちは！

前回、前々回と、分数を使った計算処理のやり方について説明しました。
今回は本題である平面図形の話に戻ります。
引き続き「面積比」について考えてみましょう！

「面積比」を考える基本は、高さ一定の「双子山」

まず、ここまでの復習をざっとしてみます。
このブログでは何度も説明しているように、「面積比」を考える基本は、高さ一定の「双子山」です。

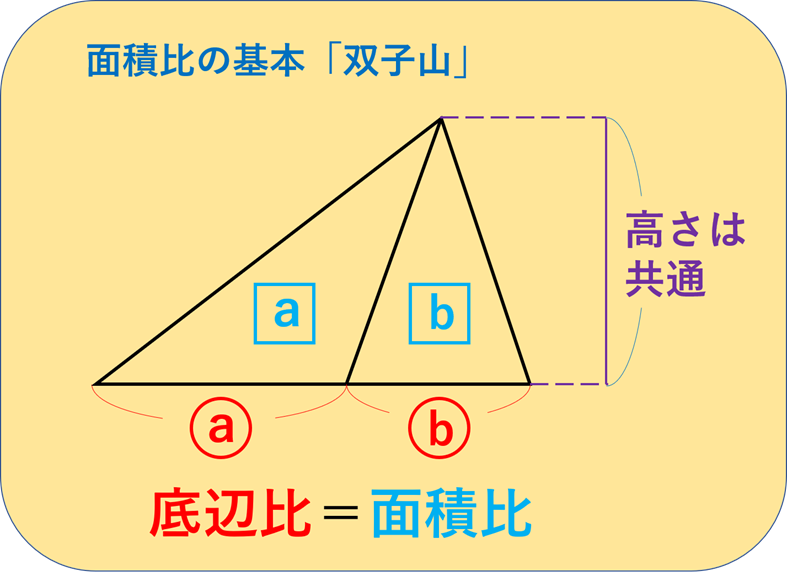
くどいようですが、とにかくこれが使いこなせることが「面積比」をマスターする第一歩です。
与えられた図の中に「双子山」が隠れていないか、常に気にしているようにしたいですね。

相似な図形の「面積比」

そして、もうひとつ知っておきたいのが、相似な図形の「面積比」です。
「双子山」は「底辺比と面積比の関係」ですが、こちらは「相似比と面積比の関係」です。
この二つがごっちゃになってしまっていることは良くあります。
それぞれをはっきり区別して、正しく使いこなせるように練習しましょう。

以上の二つを正しく使えているなら、「面積比」についてはすでに中級者の実力といっていいと思います。
ほとんどの問題がこの二つだけで解決できるので、自信を持って問題を解いてみてください。

様々な形での「面積比」についての知識

ただし、上級者を目指すなら、より様々な形での「面積比」についての知識を持っている必要があります。
今回はその第一歩として、次のような問題を考えてみます。
この問題がさっと解けますか？

この問題を「（2×4）:（5×5）で、8:25だな！」とさっとできるならOKです。
結論を先に書くと、このような形では、以下のような公式が成立します。

受験ドクターの根本原理テキストでは、実践編123番「Aをねらえ」に出てきます。
ちなみに、この公式には一般的な呼び名というのがないです。
どんなテキストにも載っていて、高校受験を含めて常識と言ってもいいものなのに、不思議ですね。

名前なんてなんでもいいのですが、説明する上ではあった方が便利ですよね。
ひとまずこのブログでは、根本原理テキストにならって「Aをねらえ型」ということにしておきましょう。

では、なぜこの公式が成立するかが、きちんと説明できますか？
説明のポイントはひとつで、「なぜ、aとc、bとdをそれぞれかけ算して良いのか」です。
これを理解するために、まずは次のように少し図を変えて考えてみましょう。

もとの図との違いはなんでしょうか？
∠Bを直角にしただけですね。
しかし、こうすると「面積比」を考えるのはとたんに楽になります。
以前も説明したように、「面積比」の基本は「たての比×よこの比」です。
∠Bが直角なら、a：bはよこの比で、c：dはたての比です。
ですから、「面積比」は（a×c）：（b×d）で問題ないですね。

しかし、こう考えてみると、「Aをねらえ型」が示していることは、以下のように言うことができます。
「このような形の場合、∠Bが何度であっても、a：bはよこの比、c：ｄはたての比と考えて良い」
わかりますか？
∠Bが直角である必要はないということです。
もちろん、実際の面積を求める場合はダメですよ！
あくまで二つの三角形の「面積比」を考える場合だけです。
しかし、「面積比」を知りたいだけなら、∠Bは何度でもあっても構わないのです。
なぜでしょうか？
これを理解するためには、以下のように補助線を引いてみましょう。

いま引いた補助線は、aとbを底辺（よこ）と考えたときの、実際の高さ（たて）です。
このときに高さの比はいくつになるでしょう？
「そうか、実際の高さも結局はc：dなんだ！」と感じた人は、相似の感覚が優れています。
なぜそういう結論になるかは、以下のように図を強調して見てみるとすぐにわかります。

わかりますか？
「ピラミッド型」の相似になっていますよね。
青い二つの三角形の相似比はc：dです。
ですから、いま知りたい補助線の比も、c：dとわかるのです。
ということで、「Aをねらえ型」の公式がちゃんと成立します。
もう一度確認しておきましょう。

高さを補助線として引くと、相似形が生まれて高さ比がわかる、という考え方はとても応用範囲が広いです。
これについては次回さらに詳しく説明します。

それでは、今日はここまでです。
また次回お会いしましょう！