皆さま、こんにちは！

 

さて、前々回・前回は、「自信と実力」や「過去問との相性」などについて、いろいろと考えてみました。

今回は、その前に３回にわたって書いていた、つるかめ算の話に戻ります。

第３回までに、つるかめ算の基本的な考え方とその重要性について説明しました。

今回は、基本さえ押さえていれば、少しひねりが入った入試問題でも十分解けるということを説明します。

つるかめ算を習いたての、たとえば４年生であっても、きちんと答えが出せるので一緒に考えてみてください。

 

【第３回までのおさらい】

第３回までに確認したことは、次の２点です。

①その問題がつるかめ算だということがわかるか

➁つるかめ算だとわかったときに、どのような処理をするか

①については、「２種類の合計が出てきている」ということが、つるかめ算かどうかを見抜くポイントでした。

➁については、書き出しや、変化を考えるや、面積図の利用、などがありました。

これら２点については、つるかめ算の学習で必ず教わることです。

ここがしっかりわかっていなければ、つるかめ算の理解はあいまいだということになります。

つるかめ算を習いたてのときは、この２点をしっかり理解できているかどうかを、丁寧に確認してください。

ポイントさえ押さえられていれば、これだけでも入試問題を解くことができます。

ためしに、次の問題を考えてみてください。

 

H23に桐朋中学で出題された問題です。

ぱっと見はつるかめ算に感じられないかもしれないですが、これは正真正銘のつるかめ算です。

まずはそこから確認してみましょう。

 

【ポイント①つるかめ算であることを確認する】

つるかめ算かどうかを見抜くポイントは、「２種類の合計が出てきている」ということでした。

では、この問題はどうでしょうか？

２種類の合計が出てきているでしょうか？

はい、ちゃんと出てきていますね。

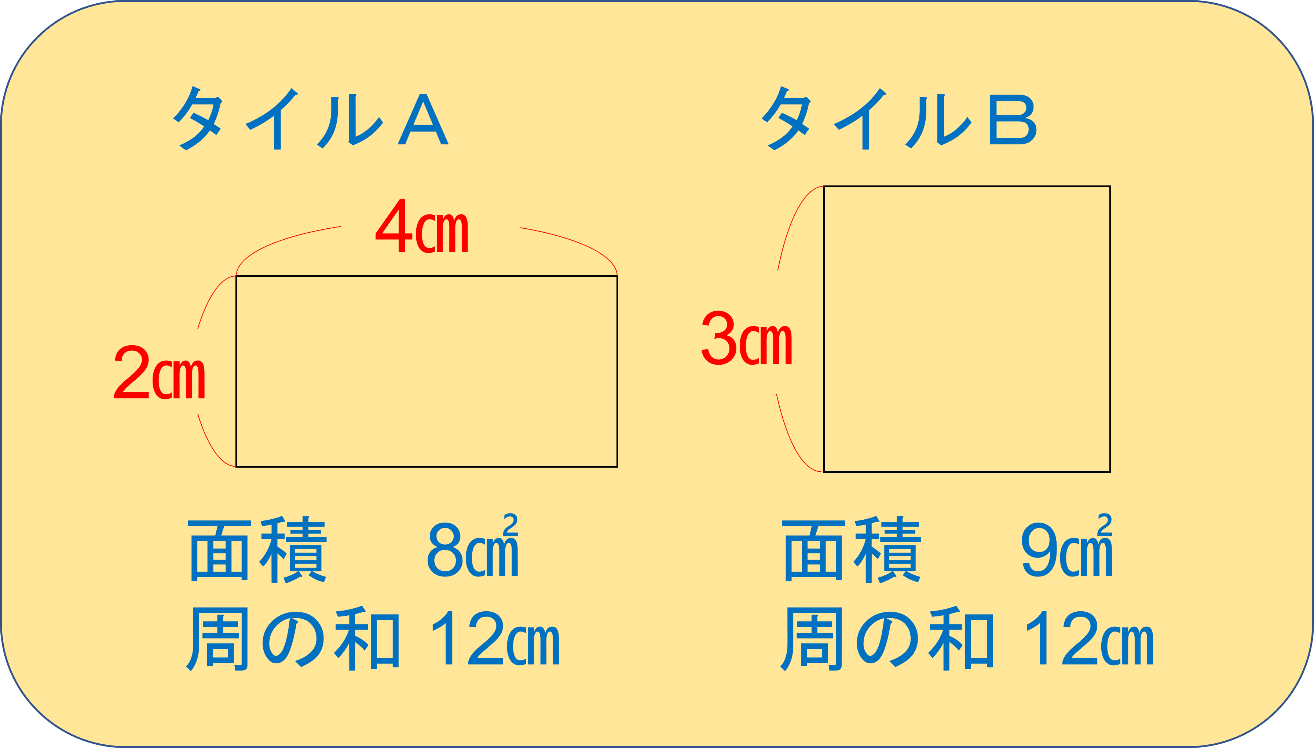
「面積の和」と「周の長さの和」の２つです。

ですから、これはつるかめ算の問題です。

ただし、少しだけひねってあります。

簡単な問題なら、頭の数と足の数や、個数と代金など、比較的わかりやすいものの合計が出てきます。

しかし、ここでは面積と周の長さとなっており、少しだけわかりにくくなっています。

まずはここで惑わされないようにしましょう。

こういうときは、一度落ち着いて状況を整理することが大切です。

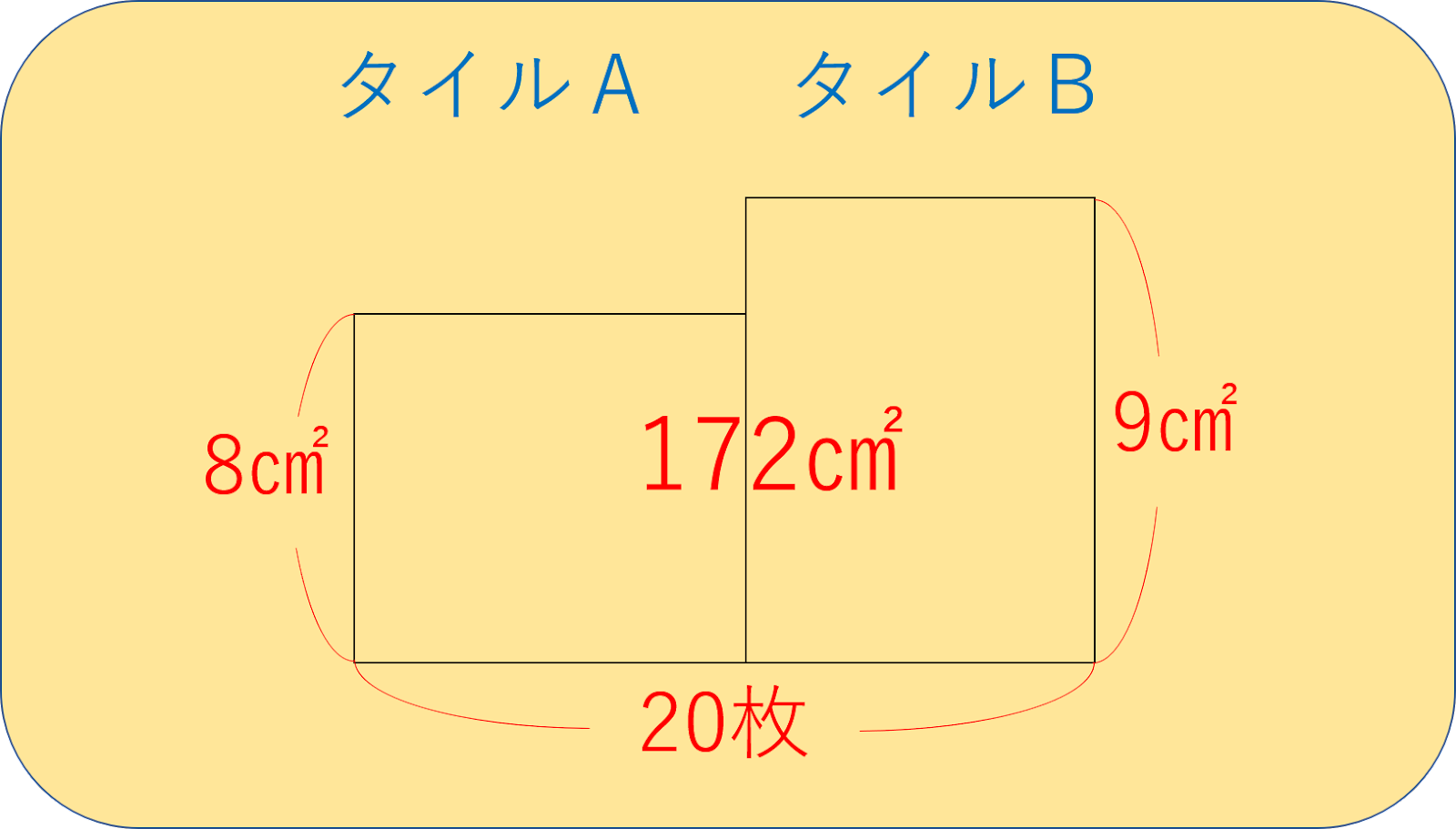
下のように簡単な図を書いて、わかっていることを目で見て確認できるように整理し直してみます。

するとどうでしょう？

何かに気がつきませんか？

そうです、タイルＡとタイルＢの周の和は同じです。

ということは、すべてのタイルの周の長さの和が240㎝ということから、タイルすべての枚数がわかるはずです。

タイル１枚の周の長さの和は１２㎝ですから、240÷１２＝２０で、タイルの枚数の合計は２０枚です。

これで、枚数の合計と面積の合計のつるかめ算に問題を変換することができ、とてもわかりやすくなりました。

ここが、この問題の最大にして唯一のポイントです。

あとは、つるかめ算の処理をすれば解決します。

 

【ポイント➁どのような処理をするか】

つるかめ算の処理の仕方は、いろいろとあります。

第２回で説明したように、表に書き出す方法もありますし、第３回で説明したような面積図もあります。

そのときもお伝えしたように、処理の仕方は自分にとってわかりやすい方法なら何でもよいです。

この方法なら自信を持って解けるという方法を、ひとつで良いので身につけておきましょう。

ここでは、前回と同様に面積図での処理をしてみます。

面積はたて×よこですから、どの要素をたてとよこに設定するかを決めましょう。

この問題の場合は、たてをタイル１枚当たりの面積、よこをタイルの枚数に設定するのが自然です。

すると、面積が表しているのは、それぞれのタイルの面積の和となりますね。

以上のことに注意して、面積図を書いてみます。

 

このような面積図が書ければＯＫです。

書きなれていないと、たての長さに面積を書いていることに、違和感があるかもしれません。

しかし、面積をよこやたての長さとして図を書くというのは、水量変化の問題の正面図でもよく出てきます。

こういう書き方もあるということに、慣れておきましょう。

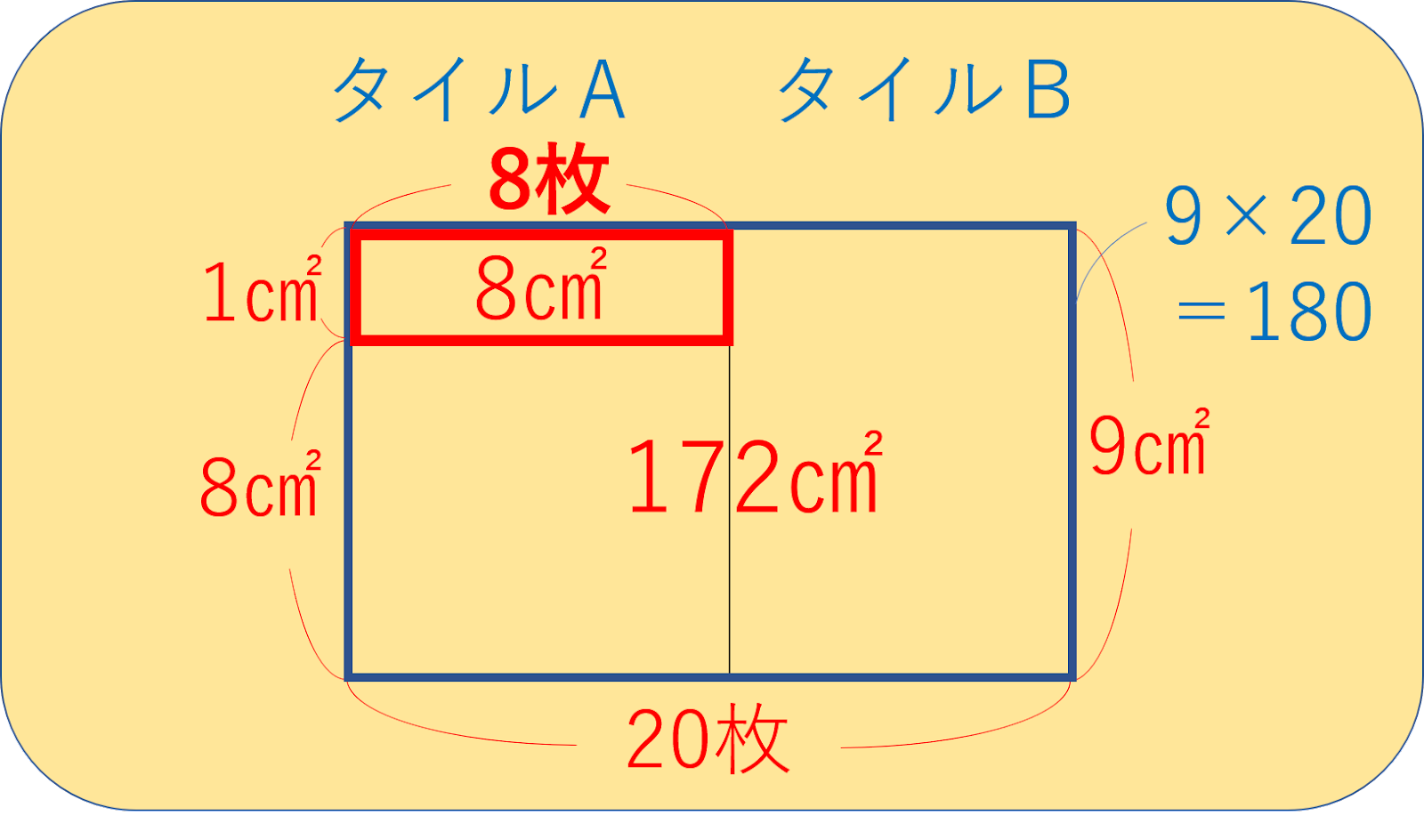
図が書ければ、あとは左上の欠けた長方形の面積に注目します。

欠けた部分を補って、全体を大きな長方形として捉えると、全体の面積は９×２０＝180で、180㎠です。

そもそもすべてのタイルの面積の合計は172㎠ですから、左上の欠けた部分の面積は８㎠となります。

９㎠と８㎠の差が１㎠ということから、赤く囲んだ左上の長方形のよこの長さは８÷１＝８で、８枚となります。

図に書き込むと、下のようになりますね。

 

ということで、答えは、タイルAは８枚、タイルBは１２枚ということになります。

前回までに学んだことで、ちゃんと入試問題も解くことができましたね！

【今回のまとめ】

以上のように、つるかめ算の基本をしっかり守れば、ちょっとした入試問題なら十分に解けるのです。

今回の問題については、「面積の和」を「枚数の和」に変換するという部分が大きなポイントでした。

このようなちょっとしたひねりをクリアできるかどうかは、様々な応用問題を解けるかどうかにつながります。

応用問題を考える際には、「どうしたら自分の知っている形に持ち込めるか？」と考えることが大切です。

算数の応用問題の多くは、基本的な問題にひとつかふたつ、新しい作業を増やすことで作られます。

ですから、どういった作業をすれば自分の知っている基本問題に戻せるかを考えることが解決につながります。

次回からは、この視点に注目しながら、様々なつるかめ算の応用問題を考えてみようと思います。

 

では、また次回お会いしましょう！