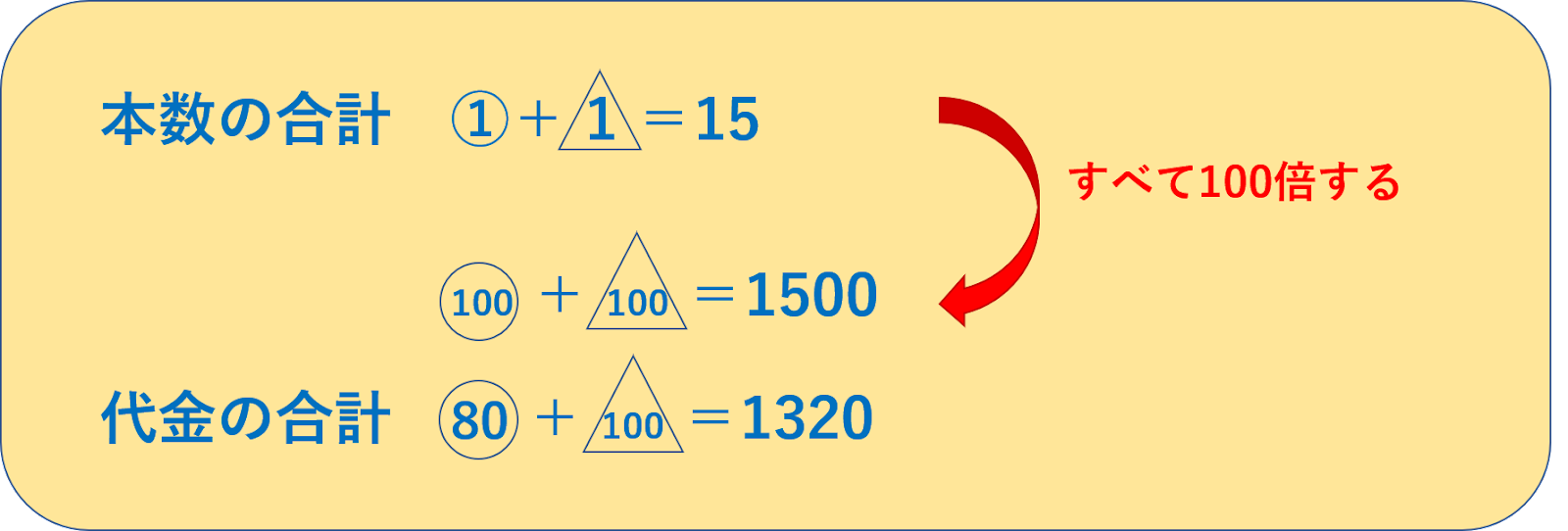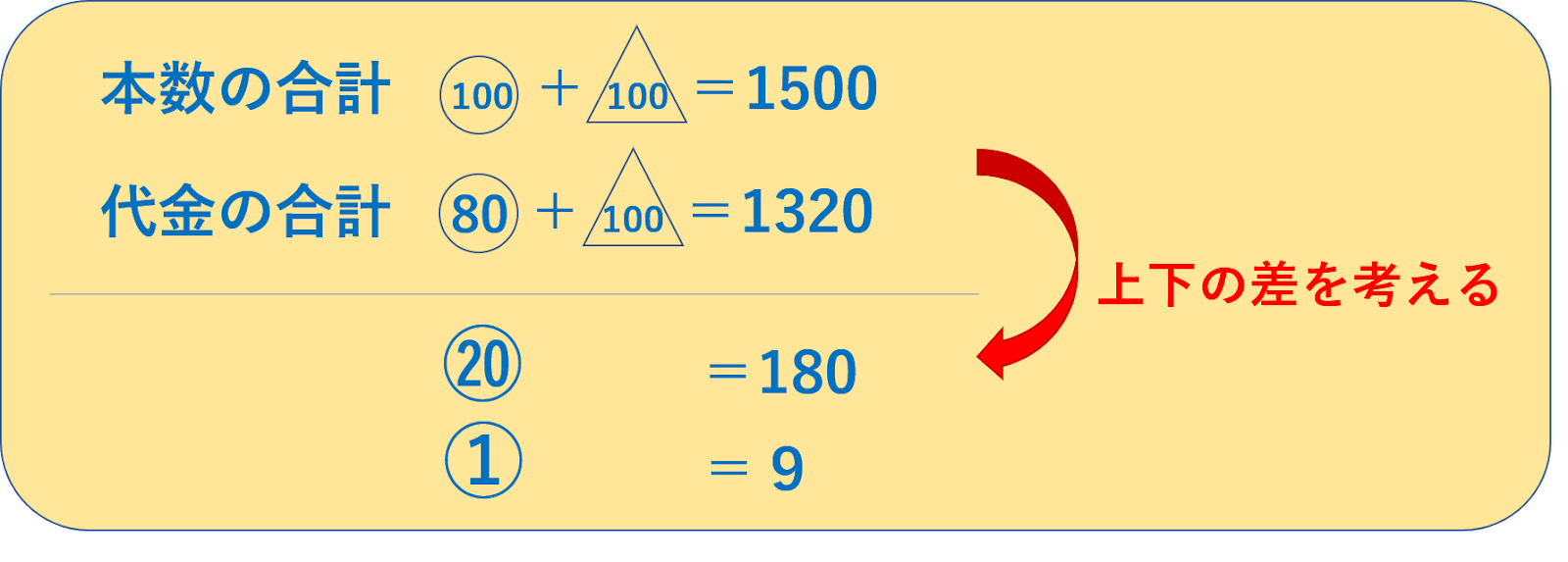皆さま、こんにちは!
ここまで6回にわたってつるかめ算の問題を考えてきました。
今回はその第7弾です。
今までとはまったく違ったつるかめ算の処理の仕方を考えてみましょう。
テーマは消去算です。
消去算は、中学2年生の数学で学習する連立方程式と本質的には一緒です。
こう聞くと、「あれ?中学受験の算数で方程式なんて使っていいの?」と感じる方もいらっしゃるかもしれません。
今回は、その辺りに疑問についても、あわせて解説します。
方程式を使ってはいけないの?
まずは、以下の問題を見てください。
これは2022年9月2日の「つるかめ算の世界③」で扱った問題です。
この問題なのですが、もし中学受験の勉強をしていないとしたら、小中学校ではいつ頃学習するでしょうか?
学校の教科書に沿って学習しているなら、中学1年生で初めて目にすることになるはずです。
1次方程式の文章題のひとつとして登場します。
さらに、中学2年生で「連立方程式」を学習しますが、その際に典型的な文章題として登場することになります。
中学2年生以降であれば、おそらくあまり深く考えずに連立方程式を使って解くと思います。
それが、高校受験に向けて勉強してきたお子さんなら当然の解き方だからです。
では、中学受験において、この問題を連立方程式で解いてはいけないのでしょうか?
答えは、問題ないです。
一般的には、算数の文章題を方程式で解くのは良くないと言われます。
入試の現場で使ってはいけない、と思い込まれているお父様・お母様もいらっしゃると思います。
つい先日も、「方程式は使ってはいけないんですよね?」とあるお母様に聞かれました。
しかし、方程式を使ってはいけない、と明言して入試を行っている中学校というのはありません。
逆に、説明会などで「方程式を使ってもOK!」とはっきり言っている学校はあります。
ですから、方程式を使ってはいけないというのは勝手な思い込みで、決してそんなことはないのです。
実際、多くの中学受験塾では、マルイチ算や消去算という処理の仕方を学習します。
マルイチ算は本質的には方程式と同じことですし、消去算は連立方程式と同じことです。
方程式という言い方をしていないだけで、同じようなことは学んでいるのです。
最近の入試問題の中にも、立式して処理することが前提になっている問題が増えているような印象があります。
もはや必須と言ってもいいくらい、当たり前の解法になっているのが現実です。
ただし、なんでもかんでも立式して方程式的に処理するのは考えものです
算数の特殊算の中には、立式しない方が簡単に解ける問題も多く存在するからです。
立式してしまうと、計算が複雑になったり、わかりにくくなったりするものも多いので、そこは注意が必要です。
算数の特殊算には問題を解くための見事な工夫や解法が多く、それを学ばないのはもったいないです。
また、お父様やお母様が方程式を使って文章題を解くことをお子様に教えるのも、あまりお勧めできません。
数学で方程式を学習する際には、その前に正負の数の概念や文字式の取り扱いなどを先に学習します。
特に負の数(マイナス)の理解は大切で、負の数がよくわかっていないと等式の操作がうまくできません。
中学受験のマルイチ算では、このあたりのことをうまく回避するように指導したり練習してもらったりします。
大人の感覚で下手に方程式を教えようとすると、逆にお子さんを混乱させてしまうという危険があります。
取り扱い注意!なものであることは間違いないので、十分に注意してください。
消去算で解いてみよう
では、つるかめ算を消去算(連立方程式)で解くことをお勧めしないかというと、そんなことはありません。
つるかめ算を立式処理することを学んでおくと、つるかめ算の応用であるいもづる算を解く際に役にたちます。
いつも書いていることですが、最終的な処理の仕方というのは、なんでも良いというのが私の考えです。
自分にとって一番わかりやすく自信のあるやり方であれば、それを使っていけば基本はOKです。
ただし、同じ問題に対しても、色々な解法や処理の仕方を知っていることは、上級者を目指すなら重要です。
様々なアイデアを自分の中に持っていることが、応用問題や初見問題への対応力につながります。
大切なことは、何事も使いどころを心得るということです。
万能な方法というものはないですし、どんなことにもメリット・デメリットの両面があります。
ということで、先ほどの問題を消去算で解いてみましょう。
XやYなどの文字式を使っても良いですが、中学受験の消去算では〇や△を使う方が一般的です。
このときに、何を〇にして、何を△にしたのかをはっきり書くように心がけましょう。
こういったちょっとしたことを算数や数学が得意な人は大切にします。
記述形式の解答の採点では、自分が何をどのように決めたのかが書かれていないと、確実に減点されます。
細かいことを面倒くさがったり、おろそかにしたりしないように心がけましょう。
今回は、鉛筆の本数を〇で、ボールペンの本数を△で表すことにします。
あとは、△と〇を含む等式を2つ作ることを考えます。
未知数が2つあるときは、それぞれを含む等式が2つ作れれば必ず答えを求めることができます。
中学生ならこのことはしっかり意識できていることが多いのですが、小学生はこの意識が少し薄い気がします。
わからないことが2つあるときは、2つ式が作れないか考える、これを合言葉にしておきましょう。
今回の問題は、本数の合計と、代金の合計の2つについて等式を作ることができます。
すると、以下のように立式することができますね。
あとは、〇か△のどちらかを1つ消すことを考えます。
これが消去算と呼ばれる理由ですね。
消し方にも色々ありますが、すべての解き方に共通することは〇か△どちらかの数をそろえるということです。
たとえば、上の本数の合計の式を100倍してみましょう。
こうして上下の式を見比べてみると、△の部分には差がありません。
ということは、〇の部分の差が合計の差の180円にあたることがわかります。
上のように考えると、①は9ということがわかりますね。
①は何を表していたかというと、鉛筆の本数でしたね。
ということで、鉛筆の本数は9本です。
鉛筆とボールペンの合計は15本ですから、ボールペンの本数は6本ということになりますね。
この答えが本当にあっているかどうか、合計代金で確認してみましょう。
80×9+100×6=720+600=1320となるので、ちゃんと合計代金は1320円になりました。
ということで、答えは鉛筆が9本、ボールペンが6本となります。
まとめと予告
今回は、今までとはまた違った形のつるかめ算の処理の仕方の紹介でした。
表を作って書き出して考える、極端な状態からの変化を考える、面積図で考える。
つるかめ算にも様々な処理の仕方がありますが、そこにまたひとつ新しい考え方が加わったことになります。
つるかめ算を入り口にして、様々な算数の考え方やテクニックが学べることが今回もわかりましたね。
消去算は少し数学的な考え方になりますが、他の分野でも応用が利く重要なテクニックです。
たとえば、速さの応用である流水算などは、消去算と非常に相性が良い問題です。
また、つるかめ算の発展であるいもづる算(不定方程式)は、立式して考えることが基本です。
消去ができない消去算という感じなので、これについては次回詳しく扱います。
では、また次回お会いしましょう!