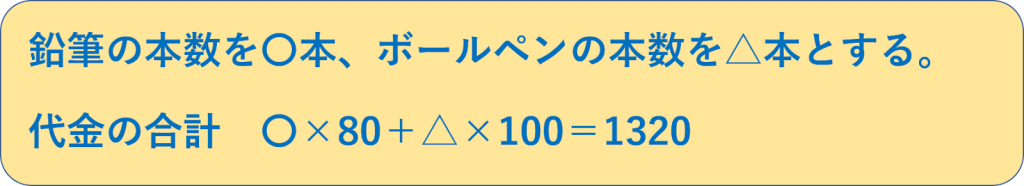皆さま、こんにちは！

 

さて、前回はつるかめ算を消去算として立式処理することについて考えてみました。
それとあわせて、中学受験の算数において方程式を利用して文章題を解くことについても解説しました。
今回はその続きで、いもづる算という問題を考えてみます。
答えが次々に「いもづる式」に出てくるのが、いもづる算という名前の由来です。
答えが次々に出てくると聞くと、「え？ 答えってひとつじゃないの？」と思われるかもしれません。
まったくその通りで、いもづる算では複数の答えが出てくるのが前提です。
条件を満たす組み合わせが何通りあるか？ということを問われることもあります。
ですから、もれなくすべての答えを見つける必要があります。
こういったタイプの問題は、難関中学では出題頻度が高いです。
有名なのは、女子の最難関中学である桜蔭中学ですね。
面白く工夫されたいもづる算が過去に何度も出題されています。
今回は手始めに、簡単な例題で考えてみましょう。

 

答えがひとつに定まらない

いもづる算の典型的な問題は以下のようなものです。

 

 

この問題を見たときに、「あれ？なんか同じような問題を見たことがあるなー」と思いませんか？
はい、まったくその通りで、前回あつかったつるかめ算の問題とほとんど同じです。
以下が前回の問題です。

 

 

まずはこの２つを見比べて、どこがどう違うかを考えてみてください。
似た問題でも、それが具体的にどう違うか考えてみると、それぞれの問題の本質のようなものが見えてきます。
今回の場合は、鉛筆やボールペンの１本の値段は一緒ですね。
そして、合計の代金は１３２０円で、これも一緒です。
しかし、鉛筆とボールペンの合計本数について、違いがありますね。
いもづる算の方は、合計本数がはっきりしていません。
つるかめ算の方は、合計が１５本とはっきりしていますね。
この部分に明確な違いがあります。

 

ここで、つるかめ算とはどういうものだったかを思い出してみてください。
「２種類の合計が出てきたらつるかめ算」だということを、このテーマの最初のブログで強調して説明しましたね。
先ほどの問題では、合計代金と合計本数という、２つの合計がわかっています。
しかし、いもづる算はどうかというと、合計代金の１つしかわかっていません。
つまり、いもづる算というのは「合計が１つしかわかっていないつるかめ算」ということなのです。
「合計が１つしかわかっていないなら解けないじゃん！？」と思われるかもしれません。
もちろん、いつものつるかめ算では解けません。
ただし、解けないというのは正しい表現ではありません。
正しくは、答えがひとつに定まらない、のです。
だから問題も、「考えられる買い方の組み合わせをすべて求めなさい」となっているのです。
では、実際に答えを求めてみましょう。

 

ひとつの等式しか立式できない

いもづる算は立式して考えるのが基本です。
前回、つるかめ算を立式して消去算として処理してみましたが、それと同じ感覚で大丈夫です。

 

 

これが、前回のつるかめ算で行った立式です。
今回は代金の合計しかわかっていないので、以下のように立式すればOKです。

 

 

ここでも、前回のつるかめ算との違いを考えてみてください。
前回は、等式が２つできていますね。
今回は１つしかできません。
わからないことが２つあるときは、２つ式が作れないか考える。
これを合言葉にしておきましょう、と前回のブログで書きました。
しかし、その合言葉をさっそく裏切るような問題が出てきたということです。
こうなると何が困るでしょうか？
前回の消去算のように、〇か△のどちらかひとつを消去するということができなくなるということですね。
ではこのような場合は、どうしたら良いでしょうか？

 

まずは探してみる

いもづる算の処理の仕方はいくつかのコツがあって、それを知っていると手早く答えを探すことができます。
ただし、答えを探さないといけないということは変わりません。
消去算のように、うまく式を処理すれば、答えがスパッと出てくるというようにはいかないのです。
コツについては、次回のブログで詳しく解説しますので、今回はあてはまる答えを探してみましょう。

 

まず、前回のつるかめ算の答えである「鉛筆９本、ボールペン６本」は答えに含まれているはずですよね？
確認してみると、９×８０＋６×１００＝７２０＋６００＝１３２０で、たしかに条件を満たしています。
これ以外に、この式を成り立たせる〇と△が見つかれば良いわけです。
たとえば、鉛筆を８本にしてみます。
すると鉛筆の合計代金は、８×８０＝６４０で６４０円となります。
すべての合計代金は１３２０円なので、ボールペンの合計代金は１３２０―６４０＝６８０で、６８０円となります。
しかし、ボールペン１本の代金は１００円なので、６８０円という合計代金になることはありえません。
ですから、鉛筆が８本の場合は、この条件は成り立たないということです。

 

ポイントは、鉛筆で減った合計代金の分、ボールペンの合計代金が増えないといけないということです。
逆も同じことで、鉛筆で増えた合計代金の分、ボールペンの合計代金が減らないといけません。
ですから、鉛筆の合計代金とボールペンの合計代金が同じ数字でないと、変化させることはできないのです。
ということは、鉛筆１本とボールペン１本の値段の公倍数がポイントになってきます。
８０と１００の公倍数は４００ですね？
鉛筆は５本で４００円になります。
一方、ボールペンは４本で４００円になります。
これが分かれば、鉛筆５本とボールペン４本が交換可能だということになります。

 

ためしに、鉛筆９本とボールペン６本というひとつの答えから、この条件で変化させてみましょう。
鉛筆を５本増やして、ボールペンを４本減らす場合は、鉛筆１４本とボールペン２本ということになります。
鉛筆を５本減らして、ボールペンを４本増やす場合は、鉛筆４本とボールペン１０本ということになります。
それぞれ合計代金が１３２０円になるか確認してみます。
前者は、１４×８０＋２×１００＝１１２０＋２００＝１３２０なので、たしかに１３２０円になっています。
後者は、４×８０＋１０×１００＝３２０＋１０００＝１３２０なので、これもたしかに１３２０円です。
これ以外は、どちらかの本数がマイナスになってしまうので、ありえません。
ということで、答えは３つあります。
鉛筆４本とボールペン１０本
鉛筆９本とボールペン６本
鉛筆１４本とボールペン２本
この３つをすべて答えられれば、正解となります。

 

まとめと予告

鉛筆９本とボールペン６本というひとつの答えから、うまく本数を変化させれば他の２つの答えが出てきました。
これが、いもづる算と呼ばれる理由です。
ひとつの答えを見つければ、あとはいもづる式に他の答えが見つかるということです。
ポイントは、ひとつの答えを見つける、そこから公倍数に注目して変化させる、の２点です。
ただし、今回の場合は基準になる答えが前回の問題からすぐにわかったので、簡単でした。
では、ひとつ目の答えをできるだけ早く見つけるにはどうしたら良いでしょうか？
これにはコツがあるので、次回詳しく解説します。
式や数字を見るときの大切な考え方が出てきます。

 

では、また次回お会いしましょう！