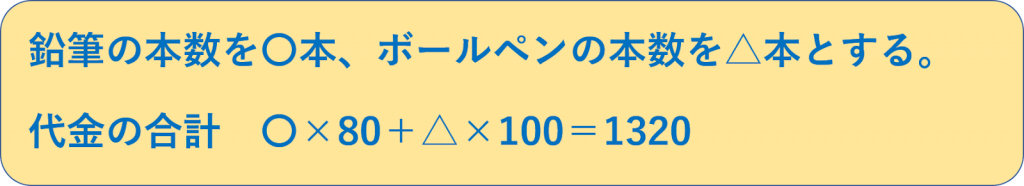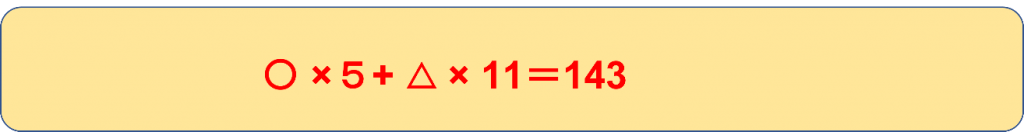【文章題】つるかめ算の世界⑨

皆さま、こんにちは！

さて、前回はつるかめ算の応用として、いもづる算（不定方程式）について解説しました。
条件の足りないつるかめ算ともいえ、答えが複数出てくるのが特徴でした。
また、答えがひとつ見つかると、そこから「いもづる式」に別の答えが見つかります。
それが、いもづる算という名前の由来でしたね。
今回は、このいもづる算において、ひとつ目の答えをどうやったら素早く見つけられるかについてお話します。

前回のおさらい

まずは前回の内容を軽くおさらいしましょう。
前回あつかった問題は以下のようなものでした。

いもづる算の基本は、与えられた文章をまずは立式してみることです。

ここから、この式を成り立たせる〇と△を探します。
前回は、「鉛筆９本、ボールペン６本」という答えはわかっているという前提で考えました。
詳しい解説は４月７日のブログを読んで頂くとして、ポイントとしては以下の２点が挙げられます。

①立式してひとつ目の答えを見つける
➁ひとつ目の答えから、公倍数に注目して変化させる

➁については前回のブログで詳しく解説しましたが、今回のテーマは①です。
そもそもひとつ目の答えを、素早く見つけるにはどうしたら良いか？
これについて、もう少し考えてみましょう。

偶奇に注目する

いもづる算の答えを見つけるコツとして、偶奇に注目する、というのがあります。
偶奇というのは、偶数か奇数かということです。
これは、いもづる算に限らず、数を扱う際にはとても大切な感覚です。
どういうことか解説してみましょう。

まず、先ほどの式をもう一度見てください。
このとき、８０、１００、１３２０は、どれも２０で割ることができますね。
いもづる算を考えるときは、できるだけ数字を簡単にした方が良いです。
等式というのは、両辺のすべての値に、同じ数をかけたり割ったりしても、イコールであることは変わりません。
ですので、すべての数字を２０で割ってみます。
すると、以下のようになります。

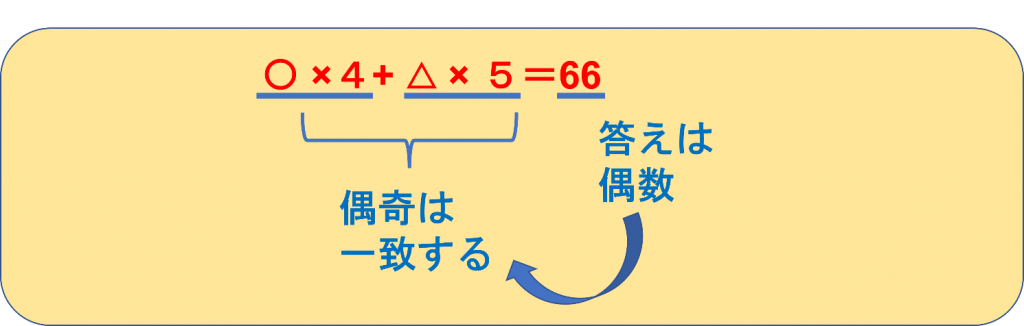
ここで、〇×４+△×５＝６６という式を見て、なにか気がつくことはないでしょうか？
ポイントは、偶数か奇数かということです。
４は偶数、５は奇数、６６は偶数ですね。
ということは、△にあてはまる数は、絶対に偶数でないといけません。
どういうことかわかるでしょうか？

ふたつの数を足して答えが偶数になるためには、ふたつの数はどちらも偶数か、奇数でないといけません。
２+６＝８や、３+７＝１０など、ためしに少し確認してみればすぐにわかります。
ふたつの数の偶数・奇数が同じになることを、偶奇が一致するといいます。
今回の問題のように、答えが６６という偶数になる場合は、〇×４と△×５の偶奇が一致しないといけません。

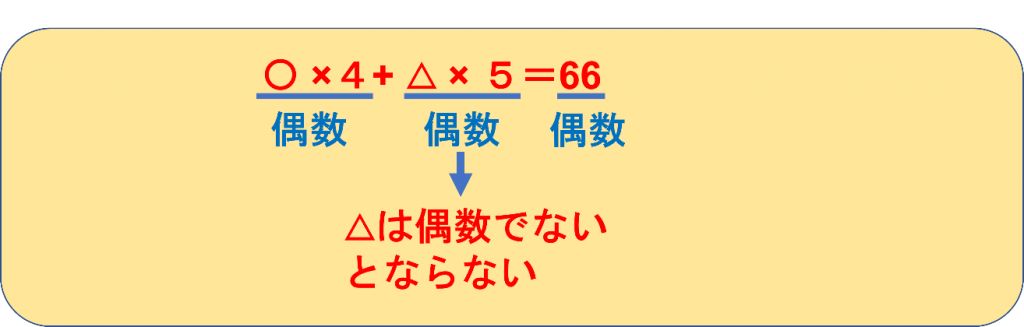
さらに、〇×４というかけ算の答えは、必ず偶数です。
どんな数に対しても、偶数をかければ、答えは必ず偶数になるからです。
〇×４が偶数だとすると、△×５というかけ算の答えも、必ず偶数になるとわかります。
しかし、△×５は、５が奇数なので、△が偶数であってくれないと、答えが偶数になることはありえません。
ですから、△にあてはまる数は必ず偶数だとわかるのです。

ちょっとしたことですが、これがわかるだけで、あてはまる数を見つける作業は楽になります。
〇にあてはまる数は、偶数でも奇数でもどちらもあり得ます。
しかし、△は絶対に偶数だとわかっています。
それなら、△の方から候補を考えていく方が、間違いなく楽ですよね？
たとえば、△が２だとしたどうでしょう？
すると、〇×４＋２×５＝６６なので、〇×４は５６になればいいです。
ということは、〇＝５６÷４＝１４です。
ですから、〇は１４、△は２なら、この等式が成り立つことがわかります。

ひとつ目の答えが見つかったので、あとは前回同様に公倍数に注目して数を変化させていけばＯＫです。
答えは、
鉛筆４本とボールペン１０本
鉛筆９本とボールペン６本
鉛筆１４本とボールペン２本
の３つですが、ボールペンの本数（△）はすべて偶数になっていますよね？
ということで、先ほど考えた「△は必ず偶数」ということは、やはり成り立っているのです。

倍数に注目する

さらに、応用として倍数に注目するというテクニックもあります。
たとえば、以下のような式ができたとします。

このとき、143という数が、１１×１３だということに気がつくと、〇と△を見つけ出すのは簡単になります。
△×１１は△がいくつでも１１の倍数になるのに対して、〇×５の方は必ず５の倍数になります。

しかし、△×１１と１４３が１１の倍数なら、〇×５も１１の倍数にならないと、この式は成立しません。
ということは、〇は絶対に１１の倍数になります。
ですから、〇の候補としては、１１か２２しかないのです。
〇が３３になると、５×３３＝１６５になり、１４３を超えてしまうので、これは考える必要がないです。
また、〇と△がどちらも０でないとするなら、これも考える必要がないです。
よって、〇が１１のときは△が８、〇が２２のときは△が３、この２つしか答えがないことはすぐにわかるのです。

まとめと予告

今回は、いもづる算の答えを見つけるコツとして、偶奇や倍数に注目するということを解説しました。
ちょっとしたことですが、答えを探す作業をぐっと楽にすることができるので、意識しておくと役に立ちます。
特に、いもづる算の難問になってくると、いくつもの条件に分けて調べる必要が出てきたりもします。
そういうときには、今回のような数の感覚を持っておくことが、スピードアップするためにとても大切になります。
いもづる算と言えば、桜蔭中学の問題が有名です。
実際の桜蔭中学の過去問を題材に、さらに複雑な問題について次回は考えてみましょう。

では、また次回お会いしましょう！