皆さま、こんにちは！

さて、前回はいもづる算（不定方程式）の答えの候補を見つける際の、ちょっとしたコツについて解説しました。

 

偶数・奇数や倍数に注目すると、答えの候補を絞り込むことができるということでした。

今回はこれを利用して、実際の入試問題で出題された少し複雑ないもづる算を考えてみましょう。

いもづる算と言えば、女子最難関のひとつである桜蔭中学がとても有名です。

桜蔭中学で実際に出題された問題にチャレンジしてみましょう。

 

【まずは立式してみる】

まずは問題を見てください。

 

 

前回までの問題と違う点は、わからないことが３つあるということです。

６個入りの菓子箱、９個入りの菓子箱、ばら売りのお菓子、それぞれの個数を求める必要があります。

大変そうに感じますが、コツをおさえればわりと簡単に解くことができます。

いもづる算の基本はまずは立式してみることでしたね。

６個入りの菓子箱の個数を〇、９個入りの菓子箱の個数を△、ばら売りのお菓子の個数を□として立式します。

すると、以下のような式ができますね。

少しでも数を簡単にするために、両辺を２０で割っておきます。

 

 

さあ、ここからこの式を成り立たせる〇と△と□を探さないといけません。

やみくもに探しても切りがないので、うまくポイントをおさえて手早く処理したいです。

 

【偶数・奇数や倍数に注目する】

まずは、前回解説した偶数・奇数という点に注目してみます。

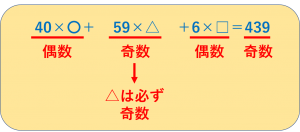
40×〇は〇がどんな数でも偶数、6×□は□がどんな数でも偶数になります。

そして439は奇数です。

ということは、59×△は必ず奇数にならないといけないことがわかります。

偶数＋偶数＋偶数の答えは偶数ですが、偶数＋奇数＋偶数なら答えは奇数だからです。

 

以上のように式を見ることができると、△にあてはまる数は1，3，5，7の４つしかありえないことがわかります。

 

△が７を超えると、それだけで439を超えてしまうので、7より大きい数を考える必要はないです。

これがわかるだけで、答えを探す作業は格段に楽になります。

あとは、この４つに関して、場合分けをしてひとつひとつ答えを確認していく作業になります。

これも大変なように感じるかもしれないですが、コツをおさえれば答えはすぐに見つかります。

ためしに、△が１の場合を考えてみましょう。

△に１をあてはめて、式を少し整理してみると以下のようになります。

 

 

上の式を見て、式を成り立たせる〇と□がすぐにピンと来ますか？

ここでも、前回解説した倍数という点に注目してみます。

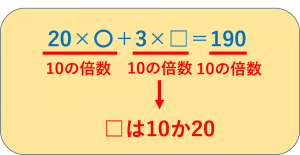
２０×〇は10の倍数で、190も10の倍数なので、3×□も10の倍数でないといけません。

□はばら売りの個数を表していますが、問題の条件でばら売りの個数は２０個以下となっています。

ですから、□の候補は１０か２０のどちらかしかありえないです。

 

 

ここまで来れば、あとは□に１０と２０をあてはめてみて確認するだけです。

□が１０のときは、〇は８になります。

□が２０のときは、〇は6.5になってしまいますが、〇は個数なので小数になってしまうのはダメです。

ということで、△が１のときは、〇は８で、□は１０しか答えがないことがわかりました。

 

【１の位に注目する】

では、次に△が３のときを考えてみましょう。

先ほどと同様に、△に３をあてはめて式を整理してみます。

すると、以下のようになります。

 

 

ここでも、この式にあてはまる〇と□を考えるわけですが、この場合はどう考えたら簡単でしょうか？

ここでは１の位に注目するという、ここまでに紹介してなかった新しいコツを使ってみます。

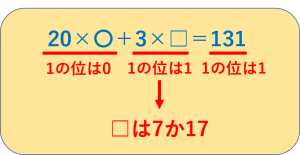
２０×〇は〇がどんな数であっても１の位は必ず０になりますね。

しかし、答えの１３１は１の位が１です。

ということは、３×□の答えは、１の位が１であるような数にならないといけないことがわかります。

 

 

よって、□にあてはまる数は７か１７です。

九九の３の段を考えてみてください。

３の段で１の位が１になるのは、３×７＝２１だけです。

ですから、□にあてはまる数は７か１７しかないことがわかるのです。

あとは△が１のときと同様に、□に７と１７をあてはめてみて確認するだけです。

□が７のときは、〇は5.5なってしまうのでこれはダメです。

□が１７のときは、〇は４になりこれはOKです。

ということで、△が３のときは、〇は４で、□は１７ということがわかりました。

 

【残りは自分でやってみよう】

△が５のときについては、ここまでお伝えしたコツを意識して、ぜひ自力で求めてみてください。

〇が３で、□が４と求められれば正しく求められています。

また、△が７のときは、この式を成り立たせる〇と□はありません。

これも、ぜひ自分自身で確認してみてください。

ということで、答えは以下の３つになります。

６個入りが８個、９個入りが１個、ばら売りが１０個

６個入りが４個、９個入りが３個、ばら売りが１７個

６個入りが３個、９個入りが５個、ばら売りが４個

 

【最後に】

いかがでしたでしょうか？

桜蔭中学の入試問題でも、正しくポイントを押さえて考えれば、答えはすぐに見つけることができます。

特に、桜蔭中学を受験するなら、今回のような作業はノータイムで反射的にできるようになる必要があります。

そこまでのレベルにたどり着くには反復練習するしかないので、頑張ってたくさん練習しましょう。

 

ここまで10回にわたって、つるかめ算の基本から応用まで順番に見てきました。

最初のブログにも書いたように、つるかめ算は他の分野の問題の中で使うことも多く、非常に重要です。

中学受験の算数の重要な基礎力のひとつなので、ぜひ理屈を正しく理解して丁寧に練習してください。

必ず様々な問題で役に立ちます。

頑張ってください。

次回からは、まったく新しいテーマを扱っていきます。

お楽しみに。

 

では、また次回お会いしましょう！