皆さま、こんにちは！

ご家庭からのよくあるお悩みについて、回答してみようという企画の第３弾です。
「やってもやっても伸びないのですが？」という、お悩みについて考えています。
前回は、１回目のブログで挙げた４つのチェックポイント
①取り組んでいるトレーニングの意味や理屈を言葉で説明できるか？
②取り組んでいるトレーニングはいまの実力や改善点に適したトレーニングか？
③取り組んでいるトレーニングの量やかける時間は適切か？
④取り組んでいるトレーニングが応用的な場合は基礎となることの理解は十分か？
このうちの、④について考えてみました。
「まさかわかっていないわけがないだろう」、と思うような基本的なことでも、実はわかっていなかったりします。
今回は、私が最近出くわした「まさかわかっていないわけがないだろう」について、さらに考えてみます。

わり算の２つのイメージ

前回は、等差数列の一般項の求め方は知っているのに、植木算は解けないというケースを紹介しました。
これについては、「まあ、そういうこともあるだろうなぁ」と感じて頂けるかと思います。
それに比べると、今回ご紹介するケースは、「まさかそんな…」と感じる部分がより強いと思います。
なぜかというと、根本的な計算に関する話だからです。
しかも、特に複雑な計算というわけではなく、基本的なわり算についての問題です。

今から説明するのは、昨年度に指導していたお子さんとの授業で実際に出くわした話です。
そこからわかっていないことがあるのかぁ…、ととても驚きました。
しかし、そのあと同じようなことがないか気にするようになると、案外いらっしゃるのですね。
実際に、今年の夏にも、２人のお子さんに同様なことが見られました。

どういうことかというと、わり算がやっていることのイメージが湧いていないのです。
もちろん、計算ができていないわけではないです。
わり算そのものはきちんとできています。
しかし、わり算というものがやっていることの具体的なイメージが思い浮かんでいないのです。
より正確には、ひとつのイメージしか浮かんでいないのです。
どういうことか具体的に説明してみます。

たとえば、１５÷３というわり算を考えてみてください。
もちろん、答えは５ですね。
では、この計算が意味していることをイメージできているでしょうか？
この計算がやっていることを絵として描いてみてください。
まず、このような絵が思い浮かんだ人がいらっしゃると思います。

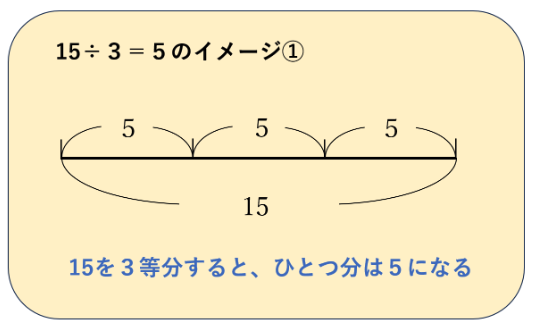
おそらく、このイメージは自然ではないかと思います。
もし、絵をひとつ描いて、と言われたら、このようなものを描く人が多い気がします。
しかし、１５÷３＝５を絵で描こうとした場合、実はもうひとつあり得るということがわかりますでしょうか？
それは、下のようなイメージです。

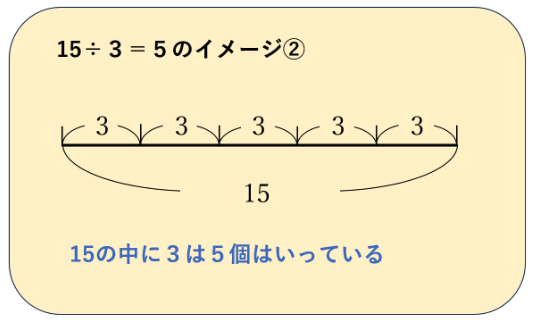
この図を見たときに、「いや、でもこれは１５÷５＝３ってことじゃないの？」と感じるかもしれません。
はい、それはそれであっています。
先ほどの「１５÷３＝５のイメージ①」（以下、図①）と同じようにイメージするなら、これは１５÷５＝３です。
しかし、この「１５÷３＝５のイメージ②」（以下、図②）も、１５÷３＝５のイメージとして間違ってはいないです。
１５÷３＝５のイメージをひとつ描いてと言われたら、人によってはこちらを描くかもしれません。
いまひとつピンとこない人がいるかもしれませんので、具体的な文章題で考えてみましょう。

たとえば、次のような問題を解く場合を考えてみてください。
問１：１５個のケーキを３人で平等に分けます。１人分は何個になりますか？
この場合、１５÷３＝５なので、ひとり分は５個になりますね。
これは、先ほどのイメージでいえば、図①のようなことをイメージしていることになります。

では、次のような問題はどうでしょうか。
問２：１５個のケーキを１人に３つずつ分けていきます。何人の人がケーキをもらえますか？
この場合も、１５÷３＝５なので、答えは５人です。
しかし、この場合は、先ほどのイメージでいえば、図②のようなことをイメージしています。

わかりますでしょうか？
この２つの問題は、どちらも１５÷３＝５なのですが、具体的なイメージが実は違うのです。
結果として同じ計算になるとしても、その計算が意味していることは、実は２つありうるということです。
しかし、こういったことを、普通はあまり深く考えずに通り過ぎていると思います。
おそらく、詳しく説明されなくても、なんとなく正しいことをやっているはずです。
私自身もこんなことを深く考えてみたことはなかったです。
昨年度の授業で、とあるお子さんに算数を教えていて、この２つのイメージについて初めて気が付きました。

そのお子さんの場合は、図①のイメージはあっても、図②のイメージがはっきり持てていませんでした。
そのため、先ほどの問２のようなタイプの問題になると、わからなくなってしまうのです。
もちろん、先ほどの問２のようなレベルの問題なら、ちゃんと解くことはできていました。
しかし、少しわかりにくくなってくるとダメなのです。
たとえば、前回も触れた規則性の問題です。

問３：３、４、５、３、４、５、３、４、５、３、…と続く数が５０個並んでいます。
５０個の数のうち、３は何個ありますか？
ひとまず答えを出してみると、考え方は以下のようになります。
考え方：この数列は「３、４、５」の３つのかたまりの繰り返しになっている。
そして、５０÷３＝１６あまり２、なので、３つのかたまりは１６個あって、さらに２つの数があまる。
ひとつのかたまりの中には、３はひとつずつだから、１６個のかたまりなら、３も１６個ある。
ただし、最後に２個余っている数のうち、ひとつは３だから、これも個数に入れないといけない。
よって、１６＋１＝１７で、答えは１７個

そのお子さんは、これが「３、４、５」という３つのかたまりの繰り返しの数列だということはわかるのです。
しかし、全体の中に、この３つのかたまりが１６個あり、さらに２個の数が余っていることがわからないのです。
説明してあげると、なんとなくは納得するのですね。
それで少し数を変えた問題をやらせてみると、それは自力ではどう計算していいかがわからないのです。
最初はどうしてそういうことになるのか、私も理由がよくわかりませんでした。
それでもしつこくやっているうちに、先ほどの図②のようなイメージがわり算に持てていないのではと感じました。

前回の話と同様で、これはたまたま気が付いただけです。
わり算そのものはできているだけに、「まさかそんなわけはないよな…」と感じることだからです。
しかし、そのまさかを疑ってお子さん自身に確認してみたのです。
すると、「そんな風にわり算というものをイメージしたことがない！」という答えでした。
そこで初めて「なるほど、そんなこともあるんだなぁ」と私も理解したのです。
そのお子さんには、わり算がやっていることの具体的なイメージからきちんと教え直しました。
やっていることのイメージとして、２つの可能性があるということを、簡単な文章題から理解し直させました。
結果として、先ほどのような規則性の問題も無事に自力で解けるようになりました。

簡単な計算のイメージから確認した方が良いかもしれない

こう書くと、「それはまた、ずいぶんレアなケースの話だなぁ」と感じられるかもしれません。
私自身もそう思っていました。
しかし、先ほども書いたように、これと同様なことを今年の夏にも２人のお子さんで経験しています。
たった２年の間に、３人のお子さんで同じことを見ているのです。
個別指導の場合、１年で担当するお子さんはそこまで多くないので、これは結構な確率です。
気がついていないだけで、もっとたくさんのお子さんがわかっていないのかもと最近は感じています。

いかがでしたでしょうか？
前回以上に、「まさかわかっていないわけがないだろう」という話ではなかったでしょうか？
３人のお子さんで同様のことを見たと書きました。
このお子さんたちに共通することは、図①のイメージはあっても図②のイメージはないということです。
算数がいまひとつ伸び悩んでいるという場合は、こういったことを「もしかしたら」と疑ってみてください。
案外、簡単な計算のイメージから実はできていないということがあるかもしれません。

次回は、なぜこういうことになってしまうのか、その原因を考えてみます。
はっきりとしたことはわからないのですが、いくつかの可能性があり得るので、それをご説明します。
今回は以上です。
では、また次回お会いしましょう。