第17回 立体の展開図
今後の目次
第17回 立体の展開図 ← 今週はココ!
第18回 複雑な設定の文章題を読み解く
第19回 正三角形を動かす
今回は、立体の展開図です。
立方体だけではなく正多面体などいろいろな立体の展開図を用いた問題もよく出題されます。
もとの立体に復元するときにどのような手法を使えばよいのか、今回はそのポイントを説明してまいります。
ポイントが身につく問題実践講座①
問題
立方体の各辺の半分の長さの点を結んで、各頂点から三角すいを切り落とすと、見取り図のような正三角形と正方形で囲まれた美しい立体図形、(アルキメデスの準正多面体)が出来上がります。

この図形の展開図は、図①、図②のようになります。

(問1)図①の展開図を組み立てたとき(A)の面と平行なのは、(B)の面です。
では、(ア)の面と平行なのは、(イ)~(ク)のどの面ですか。
(問2)図②の展開図を組みたてたとき、辺アイと平行な辺はどこですか。
図②に書き込んでください。
(1つの辺が、2つに離れている場合は、両方に線を引いてください。)
(1997 ジュニア算数オリンピックトライアル)
【解くための考え方】
まずは、先ほどの問題を直接お子様に解かせてみてください。
どうでしたか?正解にたどりつけたでしょうか?
正解できなかった場合、どこまで解き進めることができたのかが重要です。
複雑な立体になれば、頭の中で想像して組み立てることが難しくなってきます。
どうすれば立体をとらえることができるでしょうか。
今後受験Dr.では、「難問攻略イメージde暗記ポイント」カードを作成する予定です。
今回は、立体の展開図の特徴をとらえるためのポイントを1つご紹介します。
今回使うポイント
- 立体の全体図がとらえにくい
⇒【ポイントNo.34】「面と面をつなぐ辺から頂点を考える」
【ポイントNo.34】「面と面をつなぐ辺から頂点を考える」
展開図の問題で、どの頂点とどの頂点がくっつくかを考えるためには「頂点に記号で名前をつける」ことが不可欠です。
そこで、問題の立体の12個全ての頂点にA~Lの記号をつけます。

そして、正方形(A)の4つの頂点をABCDとして、展開図に書き込みます。

ここでポイントとなるのは、面と面のつながり方です。
展開図を見ると、全ての面と面は1つの辺でつながっている、ことがわかります。
つまり、同じ辺を共有する図形は必ず2つあるということです。
そこで、どの面とどの面が同じ辺でくっついているかを順に考えていきます。
たとえば、正方形ABCDと辺ABでくっついているのは三角形ABEとなりますので、展開図にEが書き込めます。


以下、同様にどの辺を共有するかを考えていきます。
辺EB・・・三角形ABEと四角形BEJF
辺FJ・・・四角形BEJFと三角形FJK
辺AD・・・四角形ABCDと三角形ADH
辺AH・・・三角形ADHと四角形AHIE
辺EI・・・四角形AHIEと三角形EIJ
辺BC・・・四角形ABCDと三角形BCF
辺CF・・・三角形BCFと四角形CFKG
辺KG・・・四角形CFKGと三角形KGL
辺CD・・・四角形ABCDと三角形CDG
辺DG・・・三角形CDGと四角形DGLH
辺HL・・・四角形DGLHと三角形HLI
辺IL・・・三角形HLIと四角形ILKJ
よって、展開図は下のようになります。

(ア)の面である三角形ABEと平行な面は、三角形GLKになりますので、ここから答えがわかります。

また、図②における辺アイは、辺BCになります。
この辺BEと平行な辺は、
辺FJ(正方形BEJFの中で、BEとFJは向かい合う辺)
辺GL(三角形ABEと三角形GKLが平行)
辺DH(正方形DGLHの中で、GLとDHは向かい合う辺)
の3本になります。
この辺を展開図の上で探すと答えになります。
【正解①】
(1)(カ)
(2)下の図

今回はもう1問、算数オリンピックから展開図の問題をご紹介します。
先ほどのポイントを使ってみましょう。
ポイントが身につく問題実践講座②
問題
A~Fのうち、組み立てても正八面体にならない展開図はどれですか。
あるだけ答えなさい。
(正八面体……八つの面が正三角形でできた立体)

(1997 ジュニア算数オリンピックトライアル)
【解くための考え方】
この問題も、先ほどのポイントを使って考えていきます。
複数ある選択肢の中から選ぶときは、共通部分を考えていくと効率よく調べられます。
① 立体の各頂点に記号をつける

② 全ての展開図に共通する部分をなるべく大きく取る
③ 共通部分に頂点をつけていく。
今回は、一番左の三角形をABCとします。

④ それぞれの展開図を調べていく。
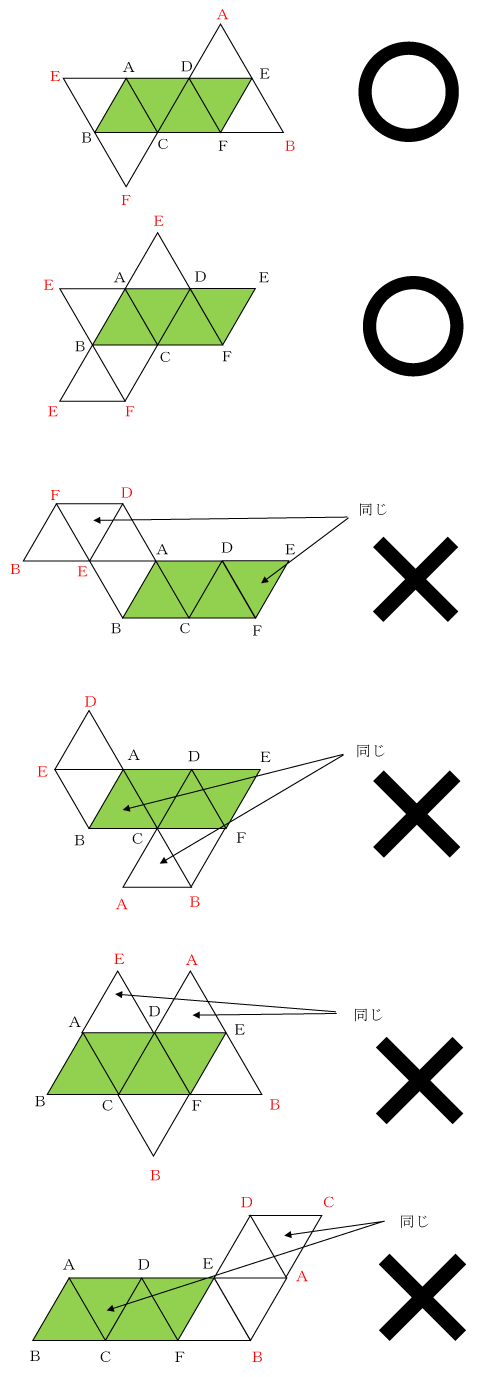
【正解②】
C、D、E、F
開成・筑駒・灘の問題で今日のポイントを使う
問題 2001 灘中(2日目)5
下の図の立体は、表面が正方形と正三角形からできている。

(問1)展開図として正しいものを下のア~カの中から選び、記号で答えなさい。

【解説】
立体としては、問題①と同じ形です。問題②で説明した、共通部分を考えてからそれぞれの展開図を考えていきましょう。←ポイントNo.34
その前に、それぞれの展開図に正三角形と正方形がいくつあるか数えてみます。
この立体の面の数は、正方形が6つ、正三角形が8つになります。
(正方形はもとの立方体の面の数だけあり、正三角形はもとの立方体の頂点の数だけあります。)
すると、オは正三角形が7つ、カは正三角形が9つあるので、この段階で間違っていることがわかります。
残ったア~エについて共通部分を考え、頂点を書いていきます。
頂点の記号は、問題①のものを使います。

ここに、正三角形と正方形を1枚ずつくっつけていきます。
正三角形から考えます。
アとエは、正方形AHIEと辺AEで、
イとウは、正方形AHIEと辺AHでくっついています。
辺AEでくっつけた場合、その正三角形はAEBになり、
辺AHでくっつけた場合、その正三角形はAHDになります。
しかし、正三角形AEBはすでに左端にくっついていますので、
辺AEに正三角形がくっつくことはありません。
ここでアとエは間違いだとわかります。
最後にくっつける正方形を考えます。
イは正三角形AHDと辺ADでくっつく正方形になりますので、
正方形ADCBになります。
ウは正三角形EIJと辺EJでくっつく正方形になりますので、
正方形EJFBになります。
正方形ADCBはすでに左上にくっついていますので、
辺ADに正方形がくっつくことはありません。
よってイは間違いとなり、正解はウになります。
答え ウ
前回のチャレンジ問題の答え
問題
下のようなマスに、0から整数を小さい順に
0、1、2、……、26、27、……
と時計の針の進む方向に渦を巻くように書き込んでいきます。

上下左右に斜めを加えた8つの方向を考えます。
たとえば、0から上の方向に3マス進んだところに27があり、
17から左上の方向に2マス進んだところに7がある、というように考えます。
(1)0から下に8マス進み、さらに右に8マス進んだところにある数は何ですか。
(2)0から上に8マス進み、さらに左に8マス進んだところにある数は何ですか。
(3)555から1マス進んだところにある数を上下左右4つの方向すべて下の図に書きなさい。

(2007 開成中 2)
【解説】
(1)
0から見て右下方向に並ぶ数字を書き出してみると、0、4、16となっています。
規則を考えるためにもう1つ右下に進んだマスの数字を書き出していくと、36になります。
ここで、4、16、36の共通点を考えてみましょう。
正これらは全て平方数(同じ数字を2つかけた答え)になっています。
4=2×2.16=4×4、36=6×6
つまり、0からみて右下に並ぶ数字は偶数の平方数になります。
したがって、右下に8個進んだ数字は16×16=256になります。
答え 256
(別解)0、4、16、36…のとなり合う数字の差を調べると、
4、12、20となっており、これは差が8の等差数列になります。
したがって、36+(20+8)=64
64+(28+8)=100
100+(36+8)=144
144+(44+8)=196
196+(52+8)=256
となります。
(2)
(1)と同様に、0から見て左上の数字を並べると、0、8、24となります。
この次にくる数字を書き出すと48になります。
0、8、24、48… のとなり合う数字の差を取ると
8、16、24…と、こちらも差が8の等差数列になります。
したがって、
48+(24+8)=80
80+(32+8)=120
120+(40+8)=168
168+(48+8)=224
224+(56+8)=288
よって、求める数は288になります。
答え 288
(別解)8、24、48をかけ算の形にすると、
8=2×4
24=4×6
48=6×8、
と連続する偶数の積になっています。
したがって、0から左上に8個進んだ数は、
16×18=288になります。
(3)
(1)と(2)の結果から555がどこにあるかを考えます。
555に近い偶数の平方数は、
22×22=484
24×24=576
また、555に近い、連続する偶数の積は、
22×24=528
24×26=624
より、0から11個左上に進んだ528と、0から12個右下に進んだ576の間にあることがわかります。
これを図にすると次のようになります。

555の正確な位置を把握するために、0から右上に並ぶ数字の規則を考えます。
0から見て右上の方向には、0、2、12、30と並びます。
となり合う数字の差を取ると、2、10、18…をこれも差が8の等差数列です。
したがって、0から右上に12個進んだ場所にある数字は、
30+(18+8)=56
56+(26+8)=90
90+(34+8)=132
132+(42+8)=182
182+(50+8)=240
240+(58+8)=306
306+(66+8)=380
380+(74+8)=462
462+(82+8)=552
552となります。
これを先ほどの図に加えると、

555は552から下に3マス進んだところにあります。
あとは、555の右マスの数字を考えるため、もう1周り外側を図に書き加えます。
552+(90+8)=650
0から右上に13マス進んだところの数字は650になります。

したがって、555のとなりのマスは上の図のとおりになります。
答え

今日のポイントを使って問題にチャレンジ!
問題
下の展開図を組み立ててできる立体の体積は何㎠ですか。
ただし三角形の面はどれも正三角形で、六角形の面はどれも1辺が2㎝の正方形から等しい2辺の長さが1㎝の直角二等辺三角形2つを切り取ってできる図形である。
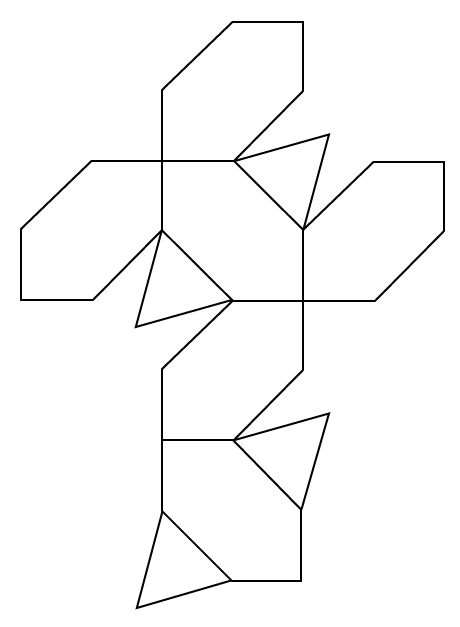
(2005 灘中(1日目)13)
※解答解説は次回掲載いたします。

