算数好きを増やしたい！！

算数好きを増やしたい！！
算数面白い！！算数大好き！！そんな子供たちを増やしたい。
そんな思いで生徒たちと接し、算数に魅了されていく生徒たちを見ると、とても幸せな気分になります。
算数は「ひとりでやってみても、できた！」という経験を手に入れた瞬間、教科自体が持つ面白みを感じることができます。
その経験が多ければ多いほど、「難問に挑戦してみようかな？」と思ってみたり、解けなかった問題があれば「なぜできなかったのだろう？」「絶対に解けるようにしたい！」など、良い方向に進んでいきます。
「ひとりでやってみても、できた！」から、「算数ちょっと面白いかも！」という気持ちが芽生えれば、自然と算数の世界にのめり込んでいくようになります。

簡単な例・具体例を用いて

算数のどんな難しい問題であれ、簡単な例や具体例に落とし込み考え直してみると、その問題の解法をひらめくことができます。
「ひとりでやってみても、できた！」という経験を与えるため、簡単な例や具体例を見せ、生徒自身が問題の解法に気づくことができるよう誘導していきます。
立体図形の切断の問題では実際に豆腐を切断して生徒たちに見せ、切り口の様子を目でも確認させるということを行っていましたが、とても評判が良く、生徒たちが驚くほど感動していたことが印象的でした。
もちろん、切った豆腐は麻婆豆腐となり、お腹の中におさまります（笑）

「ひとりでやってみても、できた！」という経験を与え、その後の学習のモチベーションを高め、様々な問題への興味を引き出し、算数好きで、算数を得点源にすることができる生徒たちを輩出していきます。

２０１８年度開成中学校の入試問題を見てみましょう。
（例題）
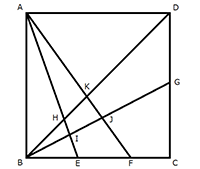
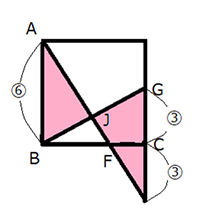
下の図において、四角形ABCDは正方形で、BE=EF=FC、CG=GDです。
三角形AIJと四角形ABCDの面積比をもっとも簡単な整数比で答えなさい。

平面図形の問題では、余分な線を見ないという考え方が重要です。
一見難しそうな問題ですが、なんてことはありません。
この問題に関しては、問題文の条件に沿って辺の比を合わせたあと、補助線を一本引き、下図のような見方をすることで問題の解き方が見えてきます。

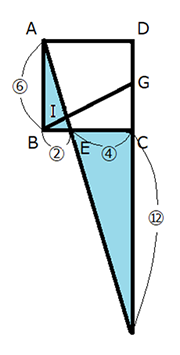
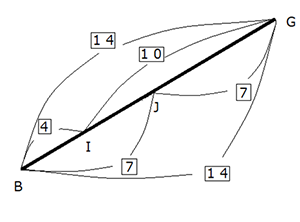
補助線AGを引き、三角形ABG（四角形ABCDの半分の大きさ）に着目すると、BI：IJ：JGの辺の比さえ求めることができれば、この問題を解くことができそうです。
まずは、下の図の青色のクロス型の部分に着目し、BI：IGの辺の比が求められないか考えてみましょう。

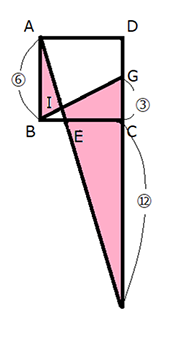
青色の部分のクロス型の辺の比を求めることで、下図のようにピンク色のクロス型の辺の比も求めることができます。

青色のクロス型の辺の比から、下図のピンク色のクロス型の辺の比を求めましょう。

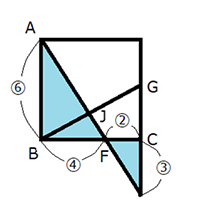
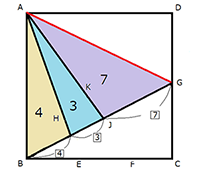
これで、BI：IJ：JG＝４：３：７という辺の比を求めることができましたので、以下の図のように三角形ABGの色分けされた部分の面積比を求めることができます。

三角形AIJ：三角形ABG＝３：１４の面積比となり、
三角形ABGは四角形ABCDの半分の大きさであるため、
三角形AIJ：四角形ABCD＝３：２８の面積比となる。

今回は、三角形ABGに着目して問題を解いてみましたが、三角形AEFに着目してもこの問題を解くことができます。
算数の問題には様々なアプローチ法がありますので、その点も教科自体の持つ面白みですね。

難しければ難しいほど、問題を解くことができたときの喜びは大きなものになります。一緒に算数を楽しみながら、志望校合格を勝ち取りましょう！！