亀井 章三先生
難しい算数も楽しく、
わかりやすく!

指導実例【算数】
多くの受験生が苦手とする「速さの問題」の解き方を、入試問題を例に説明いたします。
問題
甲陽学院中学校H26年(2日目)
川の下流のA地点から上流のB地点に向けて甲君が、B地点からA地点に向けて陽君が船を漕いで同時に出発します。甲君は45分間でB地点に到着する予定でした。
ところが、出発してから20分後に漕ぐのをやめて12分間流された後、再び漕ぎ始めたので、B地点に到着するのに1時間かかりました。ただし、川の流れの速さは一定とします。
(1)静水での船を漕ぐ速さは、陽君は甲君の0.6倍です。陽君がこの速さで船を漕ぎ続けるとき、甲君と陽君は出発してから何分何秒後にすれ違いましたか。
(2)陽君は(1)と同じ速さで出発し、途中から静水での漕ぐ速さを半分にすることにします。漕ぐのをやめている間の甲君とすれ違うためには、陽君は出発してから何分何秒後から後に漕ぐ速さを変えればよいですか。
速さの問題で大切なのは、問題文の状況を正しく捉えることです。そのために、ダイヤグラムや状況図といった図を描きましょう。
今回は流水算ですのでダイヤグラムを描いてみましょう。
図を上手に描くコツは、絵描き歌のように問題文を読みながら出てきた順に書いていくことです。そこで、問題文を区切りながら、その時点でのダイヤグラムを見てみます。
(問題文)川の下流のA地点から上流のB地点に向けて甲君が
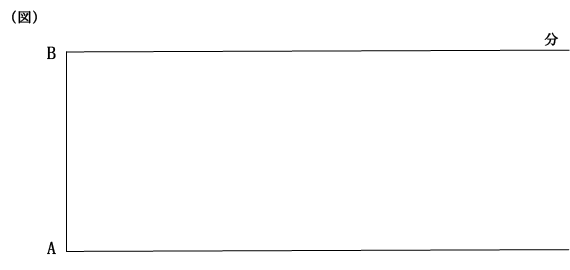
ダイヤグラムはスペースを確保し、大き目に描いていきましょう。
(問題文)45分でB地点に到着する予定でした。
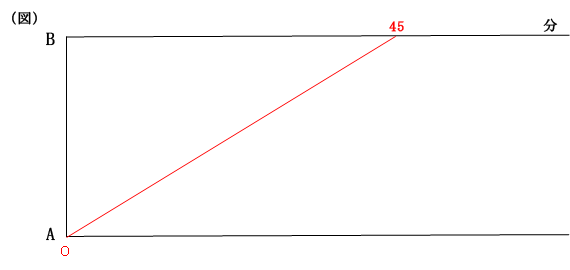
横軸は時間を書きます。上の辺にも数字を書くと見やすくなります。
(問題文)ところが、出発してから20分後に漕ぐのをやめて12分間流された後、再び漕ぎ始めたので、B地点に到着するのに1時間かかりました。
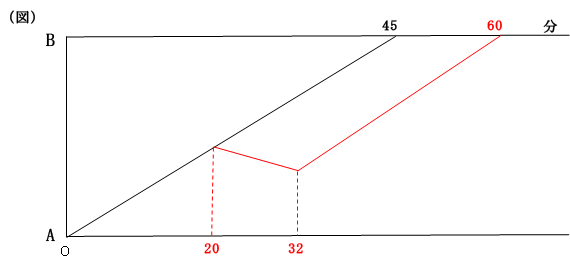
上る速さは同じなので、平行な線を引きます。
問題文を図にすると以上になります。ここからは設問を読んでいきます。
(1)静水での船を漕ぐ速さは、陽君は甲君の0.6倍です。陽君がこの速さで船を漕ぎ続けるとき、甲君と陽君は出発してから何分何秒後にすれ違いましたか。
いきなり問題を解くのではなく、答えを求めるために必要な材料を考えましょう。
今回は、ダイヤグラムを描いて考えていますので、陽君の動きがダイヤグラムで表わされると、いつすれ違ったかが詳しくわかりそうです。
では、陽君のダイヤグラムを描くには何が必要でしょうか?
それは、陽君がA地点に着くまでの時間です。陽君がB町を出発した時間は甲君と同じなので、ダイヤグラムの左上からスタートします。到着となる右下の時間がわかれば、直線を引けば完成します。
では、陽君がA地点に着くまでの時間を出すには何が必要でしょうか?
ここであわててしまうと、次のような間違いをしてしまいます。
(間違い)甲君と陽君の速さの比が5:3だから、同じ距離を進むのにかかる時間の比は逆比の3:5になる。甲君は45分でAからBに移動するので、
| 45× | 5 | = | 75(分) | |
| 3 |
普通の道だったらこれでOKですが、今回は川です。川の流れが入ってきますので、甲君の上りの速さと陽君の下りの速さの比は5:3にはなりません。
ということは、川の流れを考慮できれば陽君がA地点に移動するのにかかる時間がわかるはずです。川の速さと静水で漕ぐ速さの関係(比)が必要だとわかります。
これで正解までの道筋が決まりました。
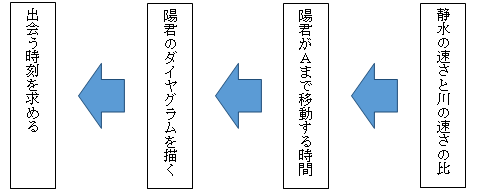
まずは、甲君が静水で漕ぐ速さと川の流れの速さの比を考えます。
速さの比を求める方法は2つあります。
① 同じ時間で進んだ「距離(道のり)の比」から求める
② 同じ距離(道のり)を進んだ「時間の比」から求める。
この問題はどちらで解けばよいでしょう。ダイヤグラムを見てみると、時間に関する情報はたくさんありますが、距離に関する情報はありません。つまり、距離の比は作れませんが、時間の比は作ることができますので、②時間の比で求める解法で解いていきます。
ダイヤグラム上で、「同じ距離」で「川が流れた時間」と「船が進んだ時間」がわかるように、次の線を描き入れます。
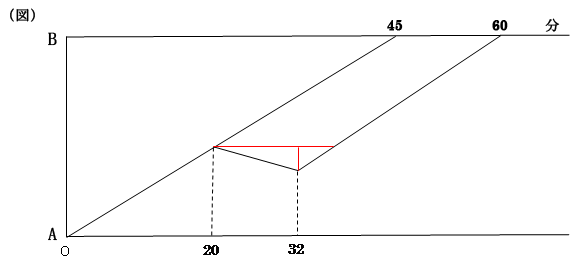
この線を描くことで、ダイヤグラムの中に平行四辺形が現れます。
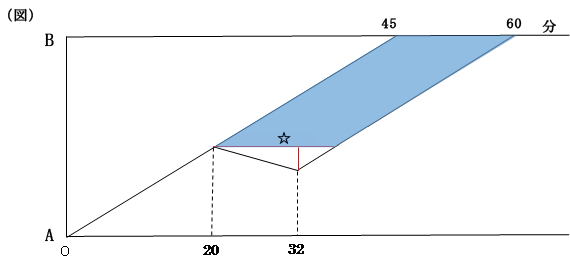
平行四辺形の特長から、☆の時間が上の辺と同じ15分(60-45)だとわかります。
よって、甲君の船が20分後に停止した場所まで戻ってきたときの時間も、20+15=35(分)
とわかります。
今わかった35分を書き加えます。

アは川の速さで12分流され、イは船が3分同じ距離を上ったことになりますので、
川の速さと船が上る速さの比は、時間の比の逆比となり、
川:静-川=1:4 となります。
よって、川:静=1:1+4=1:5 になります。
甲君の静水で漕ぐ速さ:陽君の静水で漕ぐ速さ=5:3
甲君の上りの速さ:陽君の下りの速さ=(5-1):(3+1)=4:4=1:1
陽君がAまで下るのにかかる時間は、甲君がBまで上るのにかかる時間と同じ45分です。
陽君の動きをダイヤグラムに描き入れます。
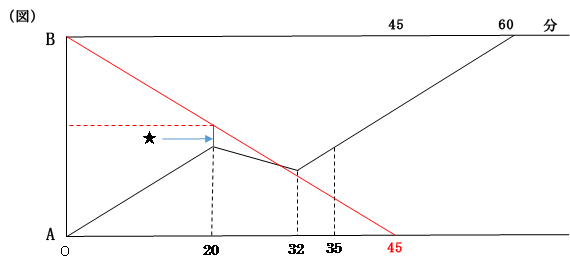
ダイヤグラムを正確に描かないと、流されている途中ですれ違ったのか、再び上っている途中ですれ違ったかわからなくなります。そういう場合は相似形ではなく、比を使って計算していくほうが確実に解けます。
20分後の二人の間の距離(★)を求めます。 甲君の上る速さ(陽君の下る速さ)を毎分④mとすると、 45×④-20×④×2=⑳が★の距離になります。 ここから甲君と陽君はそれぞれ、毎分①m、毎分④mの速さで下るので、甲君と陽君がす れ違うのに、
| ⑳÷(④-①)=6 | 2 | = | =6分40秒 | |
| 3 |
かかります。
したがって、答えは26分40秒後になります。
これは甲君が流されていた時間(20分~32分)の時間になりますので正解と言えます。
(2)陽君は(1)と同じ速さで出発し、途中から静水での漕ぐ速さを半分にすることにします。漕ぐのをやめている間の甲君とすれ違うためには、陽君は出発してから何分何秒後から後に漕ぐ速さを変えればよいですか。
まずは陽君が静水での漕ぐ速さを半分にするとどうなるか求めます。 (1)より、川の流れの速さは毎分①m、陽君の静水での漕ぐ速さは毎分③mでしたので、 ①+③×0.5=毎分2.5 mになります。
半分にすると速度が遅くなりますので、速さを変える時間が早くなればなるほど、甲君とすれ違う時間が遅くなります。イメージがつかみにくければダイヤグラムで考えてみましょう。

設問は、何分何秒後から後に…となっていますので、一番早く時間を変えた時を考えることになります。そして、一番早く時間を変えたということは、すれ違ったのが一番遅い時間であることになります。それはいつか?と考えますと、甲君が再び上り始めた32分後になります。
甲君は32分後にA地点から、20×④-12×①=68上った場所にいます。
ということは、陽君は32分間でB地点から、45×④-68= 112下ったことになります。
2種類の速さ(毎分④mと毎分2. 5 m)、合計32分、進んだ距離が112 m、という条件から
つるかめ算になることがわかればもう少しです。
2.5×32=80
112-80=32
| 32÷(4-2.5)=21 | 1 | 分= | 21分20秒後 | |
| 3 |
このように、応用問題や複雑な問題も、一つひとつ順序立てて考えていくことで正解にたどり着くことができます。特に、難関校と呼ばれる学校の問題は「一見難しそうだが、条件を整理し丁寧に考えていく」ことを求める傾向が強いです。
解法を教えるだけでなく、考え方・思考の習慣を身につけていく、そんな指導を行ってまいります。

