桑田 陽一先生
正しい努力を積み重ねよう

自分の思考回路のコピーをインストールする
中学入試算数を指導する講師であれば、まず中学入試問題が自分で解けるということは当たり前。
ということは、もし、自分の思考回路をそのまま子どもたちにコピーすることができてしまうなら、算数についてはどんな学校でも合格点を取ってもらえます。
もちろん、アプリをインストールするような形で、子どもたちの頭に講師の思考回路をコピーすることは不可能です
(近未来には出来るようになるのかも?それはそれで、ちょっと怖いですね)。
でも私は、算数の指導の理想形は、自らの思考回路を目の前の子どもたちにそのままインストールすることだと考えています。
私にとって、算数を指導するときの大目標は「自分が考えるのと同じように、目の前の子が考えられるようにすること」です。
このことを根底において、導入の仕方、言葉の選び方等に気を遣っています。
また、ある1つの単元の指導法をブラッシュアップするというレベルでなく、受験算数全体の構造を踏まえ、なるべく広い単元を統一した考え方で理解できるような指導法を常に追究しています。
もちろん、ある単元を既に充分理解できている子に対して、私の思考回路と全く同じ考え方を強制しようということではありません。
良い形で整理された思考が出来ている子に対しては、それを最大限生かしつつ、さらに大きな視野で算数全体を捉えられるように誘導していきます。
4・5年生や、6年生でも算数に自信が持てていない子に対しては、受験算数を捉える理想的な型の1つとして、私の思考回路をなぞれるようになることを到達目標に、1回1回の指導を行っています。
まずは「初期動作」を意識して覚えよう
算数の「初期動作」って、何でしょうか?
たとえばつるかめ算ならば「仮に全てを片方にそろえて、実際との差に注目する」とか、仕事算ならば「全体の仕事量を適切に決めた上で、1日(時間・分…)あたりの仕事量を求める」など、「どんな種類の問題なのかを把握したら、まず行うべき操作・作業」のことを「初期動作」と呼ぶことにしましょう。
では、「平面図形」の初期動作って何でしょう?「旅人算」の初期動作は?「流水算」や「ニュートン算」では?
算数に苦手意識を持つ子は、単元ごとの適切な初期動作が明確な形で意識できていないことがほとんどです。
単元学習中の4・5年生や苦手単元を多く抱える6年生には、根本原理の理解につながる「単元ごとの初期動作」を端的な言葉・形で示し、意識的に作業をさせることを指導の入り口にします。
「意識して」初期動作を行うということを繰り返していると、そのうち「無意識に」初期動作が行えるという段階にステージアップできるようになってきます。
算数の得意な子たちは、自然に適切な初期動作を行っているにすぎない、と言ってしまってもよいかもしれません。
念のため強調しておきたいのは、「解法の丸暗記」とは全く異なるということです。
一生懸命勉強している割に成績に表れてこないという子に多く見られるのが、○○算の問題のAパターン・Bパターン・Cパターン…のように、パターンが少し変化するごとに、ひたすら解法を覚えこむような勉強の形です。例題学習の悪いこなし方に陥ってしまっています。
○○算を解決するために必要な根本原理を包含した初期動作「だけ」をしっかり覚え、初期動作が終わった後は自分の力で考える、というのが算数の力をつける基本姿勢です。
健全な形での初期動作を蓄積していくことで、どんな子でも最終的には「初見の問題に自力で対応できるステージ」に上がれると信じて、日々指導しています。
「理科が苦手」というけれど…
「理科が苦手・嫌い」という子はたくさんいます。
でも、「理科が苦手・嫌い」って本当にそうですか?
保護者の皆さまにはお分かりの通り、小学校の理科というのは、もう少し先に進んだ立場から見ると、ずいぶん雑多な分野を寄せ集めた科目です。
高校理科の用語で言えば「物理」「化学」「生物」「地学」の4科目の内容が、とりあえず小学校の段階では「理科」の1科目に集約されているわけです。
社会では地理・歴史・公民の3分野融合問題も多くみられますが、理科の出題で、例えば「植物と力学の融合問題」なんていうのは相当に考えづらいですね。
さて、「理科が苦手・嫌い」というお子さん、小学理科の全範囲全単元にわたって、全てが等しく苦手で嫌いなんでしょうか?
「理科」という科目に苦手意識があったとしても、ほとんどの子は「ほんっとーーーうに嫌いな単元」「まずまずな単元」「割と好きな(ましな)単元」…のように、苦手意識にも単元ごとに差があるのが普通です。
「理科が苦手」とか「理科が嫌い」というざっくりした言い方は、今日を最後にやめましょう。
そして単元ごとの学習を続けている期間は、「好きな単元」「嫌いな単元」を仕分けする時期と考えてください。
「好きな単元」は単元学習の時点で、なるべく深いところまで妥協無く理解していく、逆に「嫌いな単元」は、1回目の学習の時点では「とりあえずしのぐ」くらいの感覚で構わないのです。
6年生になって、総復習・総合演習・過去問演習を通して、しのいできた苦手単元の穴を埋めていくというのが、苦手意識がある子が理科とうまく付き合った上で、最終的な勝利をつかむ道だと考えています。
ここではニュートン算を題材に、「初期動作」を意識し、根本原理から問題に取り組む例を見ていきましょう。
ニュートン算とは
ニュートン算とは、とりあえず「後から後から仕事が追加されてしまう仕事算」というとらえ方でよいでしょう。
・毎日一定量の草が生えてくる牧場に牛を放牧して草を食べつくさせる。
・一定量の水が流れ込んでいるタンクの水を空にする。
・一定の人数が新たにやってくる行列をなくす。
このあたりの設定が定番ですね。
ニュートン算というというだけで、なんとなく難しいというイメージを持っている人も多いようです。
確かに、ニュートン算を題材に難問を作ることもできます。
しかし、ニュートン算だからといって無条件に難しいというわけでもありません。
指導時の子供たちの様子や、インターネット上での「ニュートン算」の検索結果から察するに、現状、線分図を前面に押し出した解法が主流のようです。
が、そもそもニュートン算の基本構造を理解せぬまま、やみくもに線分図を書くことを覚えても、本当の理解にはつながらないと私は考えています。
まずは例題を使って、ニュートン算の構造を整理してみましょう。
例題1
2013年 佼成学園中学校
500Lの水がたまっている池に、1時間に50Lずつ水が流れこんでいます。
この池の水をなくすため、1時間で60Lの水をぬくことができるポンプAと、1時間で70Lの水をぬくことができるポンプBを使いました。
次の問いに答えなさい。
(1)(2)略
(3) ポンプAとポンプBを1台ずつ使うと、池の水をなくすのに何時間何分かかりますか。
ニュートン算の問題としては、とても基本的な問題です。
「簡単だ!」と思えましたか?
ニュートン算だから、とりあえず線分図を書くのかな?なんて考えている人もいるかもしれません。
ニュートン算の問題は、次の4つの要素で構成されています。
- ・初期在庫(初めからたまっている仕事)
- ・入荷速度(一定時間に増える仕事)
- ・出荷速度(一定時間に減る仕事)
- ・枯渇時間(仕事が完了するまでの時間)
あえて、ごつごつした言葉を使ってみました。
もちろん、指導時にはもっと分かりやすい言葉で伝えます。
中には、こういう言葉を聞いただけでワクワクする子も一定数いるのですけどね…。
さて、4つの要素を、こんな感じの図に表してみましょうか。
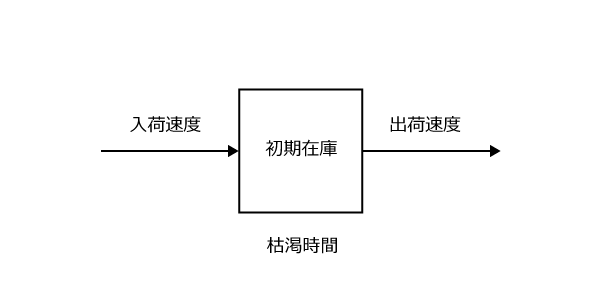
ここに、問題文に出てくる数字を適切に当てはめていきます。
500Lは、初めからたまっている水ですから「初期在庫」ですね。
50Lは1時間に増える水なので「入荷速度」に50L/時、60Lと70Lは共に1時間ごとに減る水ですから、あわせて「出荷速度」の欄に130L/時と書いておきます。
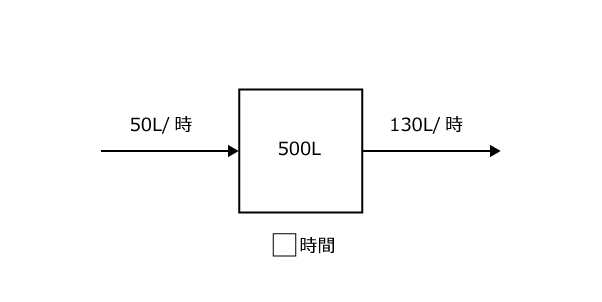
さあ、ここで分かることは何でしょう。
1時間に130L減らしつつも50L流れ込んできてしまうので、実際に1時間に減る水の量は、130-50 = 80Lということになりますね。
これも書き込んでおきましょう。

ここまで来たら、もう簡単。500Lの水が1時間に80Lずつ減っていくのですから、池の水がなくなるまでの時間は、
| 500÷80 = 6 | 1 | (時間) | ||
| 4 |
すなわち6時間15分と求められました。
このように、ニュートン算の「初期動作」は、4つの要素のうち、どれが分かっていてどれが分かっていないのかを整理することです。
例題2
2014年 法政大学中学校 1回
開園前の遊園地に64人の行列ができていて、その後も人が毎分8人ずつ行列に加わります。
入り口を1つ開くと4分で行列がなくなるとき、入り口を2つ開くと行列は□分□秒でなくなります。
やはり、先ほどの図に分かっている要素を書き込んでみます。
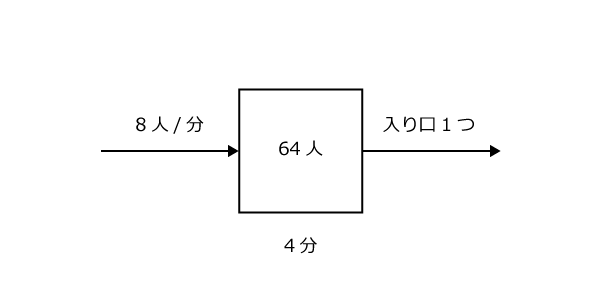
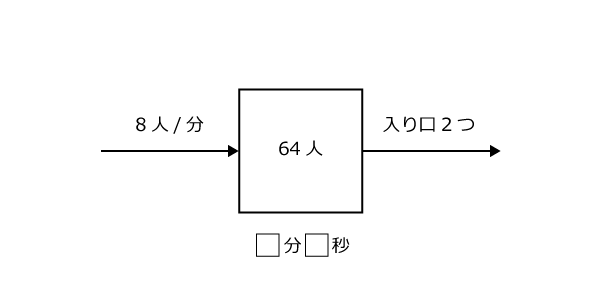
注意するのは、図が2つ必要になるということです。
この問題では、入り口を1つ開けた場合と、2つ開けた場合の、2つの状況をとらえる必要がありますね。
でも、2つの図になったからといって、それほど難しくなったわけではありませんよ。
よく見ると、初めの図については、4つの要素のうち、初めから3つが分かっている状態になっています。
このように3つが分かっているときに、もう1つを求めることは、それほど難しくありません。
やってみましょう。
初めの図について、64人の行列が4分でなくなりましたから、実際に1分で減る人の数は64÷4 = 16人/分ですね。

このことから、「出荷速度」についてどんなことが分かるでしょう?
そう、8人ずつ行列に加わっているにもかかわらず、16人減るのですから、1つの入口では、8+16=24人/分ずつ「出荷」していることになりますね。
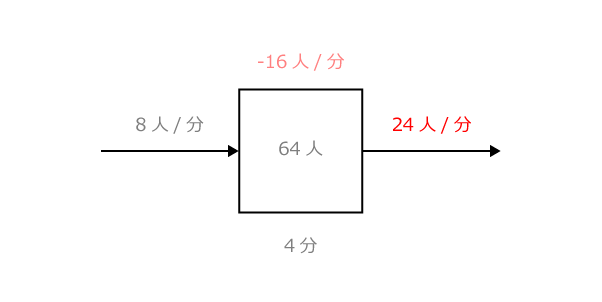
このことから、2つ目の図の空欄をもう1つ埋めることが出来ますか?
2つの窓口を開けたのですから、いま求めたばかりの24人/分の2倍、すなわち48人/分出荷されていくことになります。
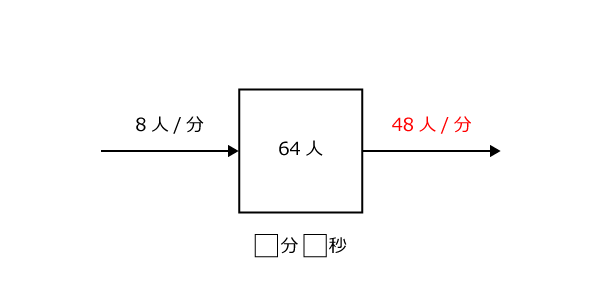
これで、2つ目の図も3つの要素が分かっている形になりました。あとは簡単!

48-8 = 40人/分が実際に減っていく人ですから、
| 64÷40 = 1 | 3 | 分 = 1分36秒 | ||
| 5 |
と求めることが出来ました。
このように、ニュートン算は4つの要素で構成されていること、そのうち3つが分かってしまえば、もう1つを求めることは簡単であるということ、これらを意識できると、ニュートン算だからといって無条件に難しいという思い込みから脱却できるのです。
例題3
2013年 東邦大学付属東邦中学校
大きなタンクに、毎分一定の量の水が入り続けています。
タンクの水が1080リットルになったときから、ポンプで水をくみ出します。
2台のポンプで水をくみ出すと2時間でタンクはからになり、5台のポンプでくみ出すと40分でからになります。
どのポンプも1分間にくみ出す水の量は同じです。
このとき、次の問いに答えなさい。
(1) ポンプ1台で毎分何リットルの水をくみ出しますか。
(2) タンクには、毎分何リットルの水が入り続けていますか。
(3) 30分以内にタンクの水をからにするには最低何台のポンプが必要ですか。
例題2と同じように、ポンプが2台のときと5台のときで、2つの状況があるので、図も2つ書くことになります。
これまでと違うのは、入ってくる水の量やポンプがくみ出す水の量が具体的な数字で分かっていないということ。
このことがだいぶ難度を上げています。
このようなときには、1分間に入ってくる水を仮に1、ポンプ1台が1分にくみ出す量を仮に1としてみるのがポイントです。
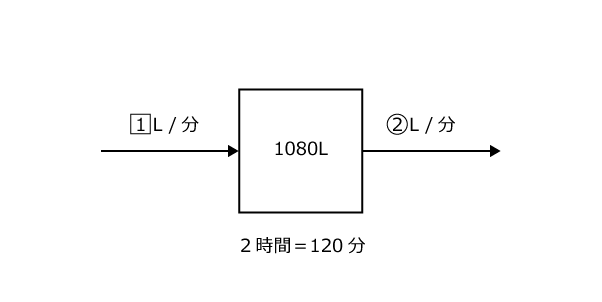
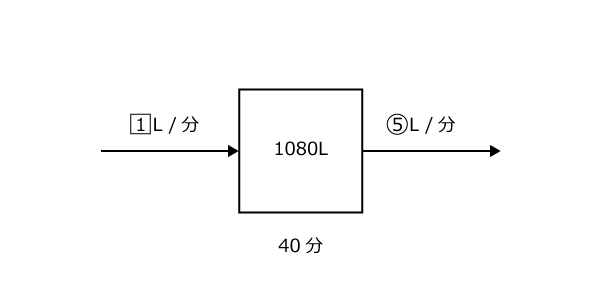
さて、ここでそれぞれの図を見て、何か計算できることはないでしょうか?
1つ目の図では、1080Lの水が120分で無くなったのですから、1080÷120 = 9L/分と計算してみると、これは「実際に減る」水の量を求めたことになります。

同様に2つ目の図では、1080÷40 = 27L/分と計算できますね。

これらの図を見て、何か感じられるでしょうか。
受験算数ではまず「わかさ」に注目。
「若さ」ではありませんよ、「和か差」です…。
1つ目の図から、2-1 = 9L/分、2つ目の図から、5-1 = 27L/分であることが分かりますね。
すると差のほうに注目して、3 = 18L/分、つまり1 = 6L/分であることが出ました。
ん、これは(1)の答えですね!
○囲みの数字が具体的な数として求められたので、すかさず図に書き込むとこんな感じ。
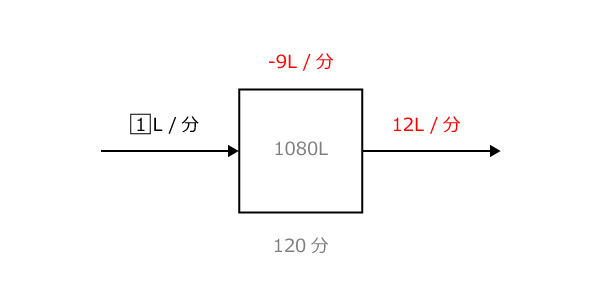
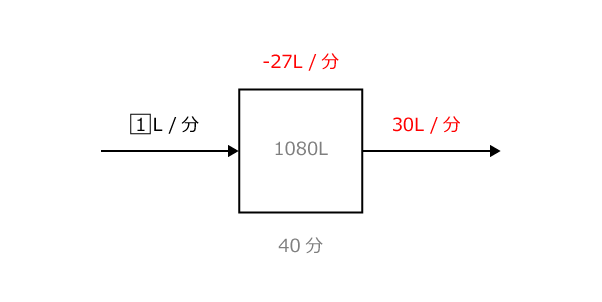
もう、どちらの図にも充分な情報が入っています。
たとえば上の図の赤字に注目すると、1 = 12-9 = 3L/分。
これは(2)の答えを求めたことになります。
さて(3)、「30分以内にからにする」という新しい状況ですので、3つ目の図を書きます。
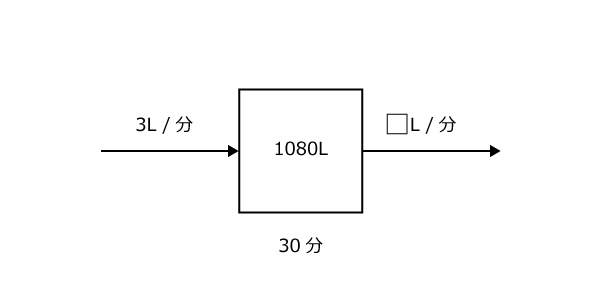
何台のポンプが必要かということは、「出荷速度」が不明だということです。
そのかわり(2)の答えから、「入荷速度」はもう分かっていることに注意。
結局のところ、3つが分かっているので簡単ですね。
1080÷30 = 36L/分、36+3 = 39L/分と「出荷速度」も求められましたか?
(1)より、1台のポンプが6L/分であることも分かっていますから、39÷6 = 6.5、つまり6台では足りず、7台が答えとなります。
このようにニュートン算の問題では、後半の設問ほど分かっている条件が増えて簡単になる、ということが結構あります。
マスターしておけば大問まるまる得点できるということですね。
普通は、後半ほど骨のある問題になっていることを考えると、ニュートン算はマスターすると差のつけやすい単元といえるかもしれません。
例題4
2014年 明治大学付属中野中学校1回
ある草原で牛を放牧します。
6頭放牧すると30日間で草を食べつくし、10頭放牧すると12日間で草を食べつくします。
このとき、次の問いに答えなさい。
ただし、草は毎日一定の割合でのびるものとし、すべての牛が1日あたりに食べる草の量は同じものとします。
(1) 何頭までなら草原の草を食べつくされることなく、牛を放牧することができますか。
(2) 6日以内で草原の草を食べつくすためには、牛は最低何頭必要ですか。
これは、充分な練習をしておかないと難しいでしょう。
「初期在庫」も具体的な数字ではなくなっています。
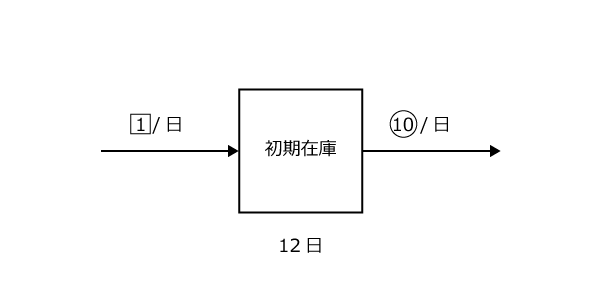
とりあえず、例題3にならって書き込めることだけ書き込んでみましょう。
例題3と同じように処理するには、1日に生えてくる草を1、1頭の牛が1日に食べる草を1とするのが良さそうですね。
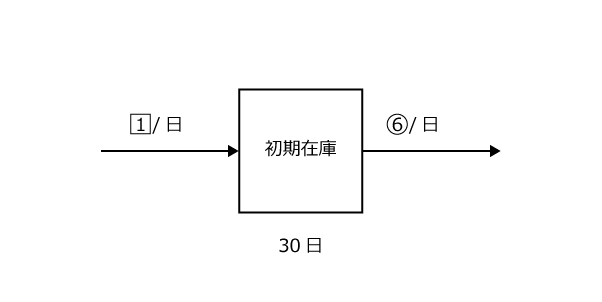
ニュートン算を充分理解できたら比を利用した省力解法もあるのですが、ここでは分かりやすさを重視して、やや計算量の多い解法でやってみます。
上の図で、1日に1の草が生えてくるので、30日間では1×30 = 30生えてきます。1日に6の草が食べられるので、30日間では6×30 = 180食べられることになります。
下の図では、1×12 = 12と10×12 = 120。
これらを、こんな風に書き込んでみましょう。

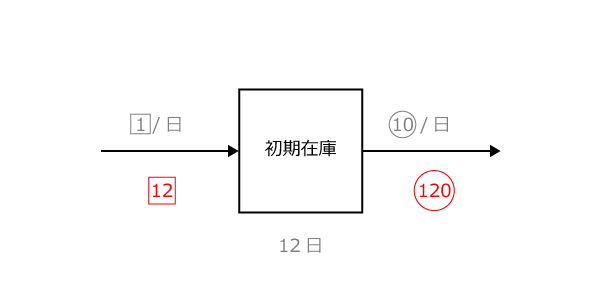
ここからは、やはり差に注目するのがポイントです。1つ目の図では、「初期在庫」に加えて新たに生えてきた30を含めて食べつくす量が180と考えられますから、
「初期在庫」+30 = 180 あるいは 180-30 =「初期在庫」
ということが分かります。同じように2つ目の図で考えれば、
「初期在庫」+12 = 120 あるいは 120-12 =「初期在庫」
さて、これらの式の差に注目して30-12 = 180-120、つまり18 = 60ということに気がつくことができたでしょうか?
割とすんなりと気がつけたのならば大丈夫。
もし、この辺の議論に理解しづらいところがあるようであれば、そこで初めて補助的に線分図を書いてみるくらいでちょうど良いでしょう。
さて、18 = 60から、3 = 10さらには
![]()
となりますね。
この最後の式が意味するのはどんなことになるでしょうか。
1は1日に生えてくる草、1は1頭の牛が1日に食べる草を表していましたから、
![]()
というのは「1日に生えてくる草は、
| 3 | 1 | 頭 | の牛が1日に食べる草にあたる」ということです。 | |
| 3 |
| つまり、牛の数が3 | 1 | 頭 | であれば | |
| 3 |
生えてくる草と食べられる草がちょうどつりあって、草原の草は増えも減りもしません。
実際には「1/3頭の牛」なんてものを放すわけにはいかないので、3頭までなら草原の草は食べつくされないことになります。
これで(1)が解決できました!
(2)はどうするか。3 = 10から30 = 100や12 = 40と表せるので、先の図の□囲みの数字をすべて○に置き換えてみましょう。

180-100 = 80と「初期在庫」が求まりました。
これを元に、「6日以内で食べつくす」という新しい状況に対応する図を書きます。
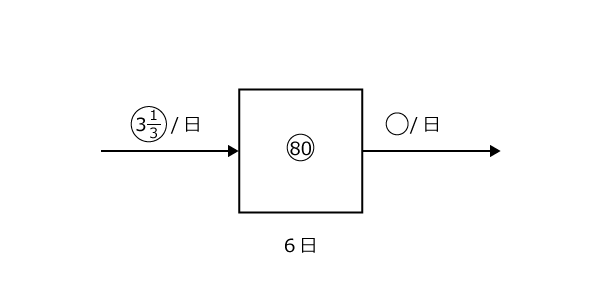
具体的な数字ではありませんが、3つの要素が分かっている形になりました。
![]()
![]()
と順に計算して、出荷速度が求められます。
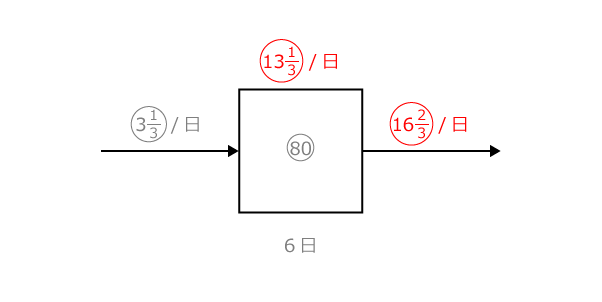
| 16 | 2 | 頭 | の牛は放牧できないので、 | |
| 3 |
切り上げて17頭と求められました。
まとめ
繰り返しになりますが、ニュートン算の初期動作は「4つの要素のうち、どれが分かっていてどれが分かっていないのかを整理する」ことでした。
このように、ニュートン算に限らず、単元ごとに初期動作を意識して問題に取り組むことが苦手意識の払拭や真の応用力につながる第一歩と考えて指導しています。

