澤田 重治先生
科学に裏付けられた効率的な学習を!

「継続は力なり」と言いますが、楽しくなければ続きません。また、「好きこそものの上手なれ」という諺にもある通り、好きになることが学習の最大のコツなのです。これは、脳科学でも証明されています。しかし、「だから楽しもう! 好きになろう!」と言われても、今まで苦手だった科目を急に好きになるなんてできるはずがありません。では、どうすれば好きになれるのでしょうか。
実は、学習でも、スポーツでも、芸術でも、上達するための手順というのはどれもほぼ同じで、大まかには以下のような流れになります。
- ①模倣……まずは、上手な人のやり方をそのまま真似してみます。
- ②反復……真似したやり方を何度も繰り返すうちに、必要な筋力や感覚(基本)が身に付いてきます。
- ③工夫……より自分の体格や性格に合ったやり方に改良(カスタマイズ)します。
- ④発展……様々なシチュエーションに対応(応用)し、自在に形を変えられるようになります。
- ⑤完成……他人に教えられるくらい、確実に身に付きます。
つまり、この流れを意識的に作り出すことで、必ずお子さんの学力を向上させることができるのです。そのため、私は次のような指導方針で取り組んでおります。
1.様々な問題に共通する「根本原理」を手本として示す
お子さんに示す手本が悪ければ、その後の上達は見込めません。また、多様化している(ように見える)中学入試の問題に対して、すべての解法を覚えさせることは不可能です。
だからこそ、その基本をきちんと理解し、柔軟に変容させることによって様々な問題に対応できるような根本原理を手本として示してあげることが必要なのです。
そして、それらの公式を「丸暗記する」のではなく、「自分で作り出せる」ようにすることを大切にしています。
2.励まし、見守り、褒めて、一緒に乗り越える
上記「上達の手順」の中で、最も苦しいのが「②反復」です。これは、スポーツでいうなら「筋トレ」や「素振り」にあたる基礎訓練の部分であり、たいていの場合、習得できるか否かの分岐点はここにあります。
だからこそ、乗り越えられるという希望を感じさせてあげること、その苦しみを理解してあげること、苦難に立ち向かう勇気を褒めてあげることが絶対に必要です。この苦しい場面でお子さんに寄り添い、一緒に乗り越えてあげられることが、個別指導の最大のメリットでしょう。
3.お子さんの「クセ」に合わせてカスタマイズする
一流のプロ野球選手を見ても、みなバッティングフォームは違います。それは当然のことで、背の高さや体格、筋肉の付き方などが異なるのですから、それぞれの個性を活かす方法も自ずと違ってくるのです。
それは、学習においても同じことでしょう。お子さんの性格や考え方がみな異なるのですから、同じ根本原理を与えても、捉え方や感覚はそれぞれ異なっていて当然なのです。
だからこそ、お子さんの考え方のクセを見抜き、できるだけお子さんの感覚にフィットする方法で指導してあげる必要があります。確かに、自分で工夫し、カスタマイズできるようになることは理想ですが、まだまだ自己分析などできるはずのない小学生に独力で乗り越えさせるにはあまりに高い壁だからです。
4.適切な時期に、適切なつながりを見せる
算数では、多くの問題に「別解」が存在します。もちろん能率の良い解き方ばかりではありませんが、いずれにしても、一つの問題に対して複数の解法が存在しているのです。これは、基礎となる「根本原理」にも多面性があり、様々な類似点によって互いにつながっているということにほかなりません。そして、この多面性によって、より多くの問題に対応できる「応用力」が生まれるのです。
また、人間は単独で覚えた知識よりも、様々なことに関連させ、ネットワークを作った知識の方が忘れにくく、思い出しやすいと言われています。応用力のためばかりでなく、使える知識にするためにも、知識の関連付けは欠かせません。
お子さんを混乱させることなく、この「知識のネットワーク」を作り上げるためには、お子さんの理解・定着の進度を見計らって、適切な時期に関連事項を示してあげる必要があります。
5.最後は「自分の言葉」で説明させる
お子さんが学習したことを自在に使いこなせるようになったか否かを確認する一つの目安は、「自分の言葉で説明できるか」です。テキストに書いてあることを丸暗記してもきっと忘れてしまうでしょうから、それでも思い出せるように準備しておくのです。
そのために、極力自分の言葉で説明させる機会を作るように仕向けています。もちろん、内向的なお子さんの場合には、分かっていても発言できないこともあるでしょうから、求めるレベルや方法はお子さんによって変えていますが、「一方的に説明して終わり」という形には絶対にしません。
最後に……これらの指導方針を根本で支えているのは「お子さんを観察・分析する目」です。
私の講師としての座右の銘は「生徒の顔は信号機」です。これは、今から二十数年前、私が講師になった時に、師と仰ぐ人からもらった言葉でした。お子さんの表情をきちんと観察していれば、そこにはお子さんの心の中がきちんと表れています。そして、赤信号が出ているのに、それを無視して進んでしまうと事故が起こるのです。
その言葉を胸に、これまで2000人を超えるお子さんを指導してきました。その中で培った観察眼、お子さんを分析する目があるからこそ、最も効果的な指導ができると自負しています。
これからも、お子さん一人一人をよく観察し、最善の処方箋を書いていきます。
【理科】楽しく学んで「記憶の脳」を活性化させる
理科や社会は、よく暗記科目と言われます。もちろん、丸暗記だけでは決して成績は上がらないのですが、それだけ記憶が重要だということなのでしょう。私の指導方針をご理解いただくためにも、まずは記憶のメカニズムについて説明させていただきます。
人間の記憶は、脳の中でも主に「海馬」と呼ばれる部分で行っています。学習に関する記憶だけでなく、自分の住所も、好きな子の名前も、サッカーのルールも、すべてこの海馬で記憶しているのです。同じところで覚えているのに、覚えやすいものと覚えにくいものがあるというのは不思議ですよね? この秘密は、海馬に隣接する「扁桃核」という脳の存在にあります。
扁桃核は、「感情の脳」と言われているのだそうです。つまり、今の自分の感情が「快」なのか「不快」なのかを判断し、それを周辺の脳に伝達する役割を持っているのです。この時、脳内物質を分泌することで伝達を行なっているのですが、扁桃核に接している海馬は、その分泌物の影響を強く受けることになります。そして、「快」の感情の時はより活発に活動し、「不快」の感情の時にはあまり活動しなくなるようです。だから、好きなものに関する知識はスラスラ記憶できるのに、嫌いなものに関する知識は努力してもなかなか覚えられないのです。
理科が嫌いなお子さんは、理科のテキストを見ただけで扁桃核から「不快」の脳内物質が分泌されてしまいます。そして、その影響を受けて不活性になった海馬で何時間勉強しても、苦痛を感じるばかりで、一向に知識は蓄積されないのです。むしろ、「努力したのに成績が上がらない」という虚無感からさらに理科が嫌いになり、次の学習でも不快になるという負の連鎖を繰り返していくことになります。
苦手な理科を得意にするには、この負の連鎖を断ち切らなければなりません。人によって興味の対象は異なりますが、それでもそのお子さんが「快」と感じられるフィールドと理科との接点を見つけ、そこから理科のおもしろさを教えていかなければならないのです。その作業は、個別でなければなかなかできないでしょう。
私の講師としての座右の銘は「生徒の顔は信号機」です。道を歩く時、信号を見ずして交差点を渡れないのと同じように、生徒に授業をする時には、生徒の顔を見なくては先に進めないと思っています。お子さんの顔は、私の話に興味を持ち、説明を聞く準備が整ったときに初めて青信号になります。 つまり、効率よくお子さんの成績を上げられるか否かは、お子さんの興味のツボをいかに早く捉えられるかにかかっているのです。そのために私は、常に多くの雑学知識を得る努力をしています。引き出しが多ければ多いほど、お子さんの興味との接点を作りやすいからです。多くの趣味も、様々なお子さんと共通の話題を持つことに役立っています。
以上のことから、「興味を持たせ、楽しく学んでもらう」というのが、私の理科の指導方針です。好き嫌いが分かれやすい科目であるからこそ、その本当の楽しさ、面白さを知ってほしいと思っています。
平成25年度(2013年度)女子学院中 大問5 に挑戦してみましょう。
問題
① ~ ⑤ にあてはまる数を解答欄にかきなさい。円周率は3.14とします。
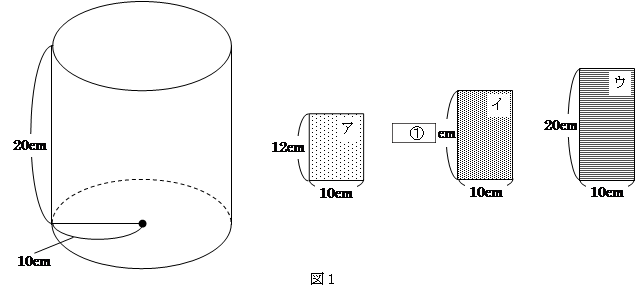
図1のような,底面の円の半径が10cm,高さが20cmの円柱の形をした水槽(そう)と,3枚の長方形の仕切り板ア,イ,ウがあります。
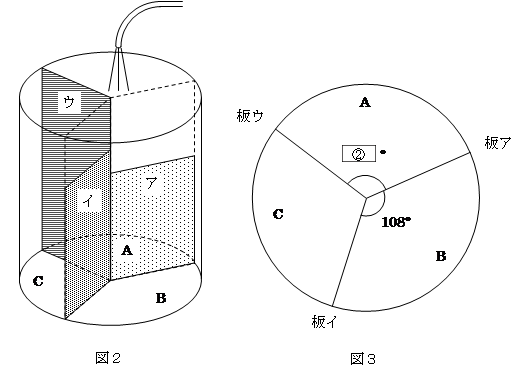
図2のように,仕切り板を底面に垂直にぴったりと入れて,A,B,Cの3つの部分に分けました。図3は,水槽を真上から見た様子です。水槽と仕切り板の厚みは考えないものとします。
水をAの部分から毎分314㎤ずつ入れると,やがて水は仕切り板アをこえてBの部分に入り始め,次にCの部分に入り,最後は水槽いっぱいになりました。
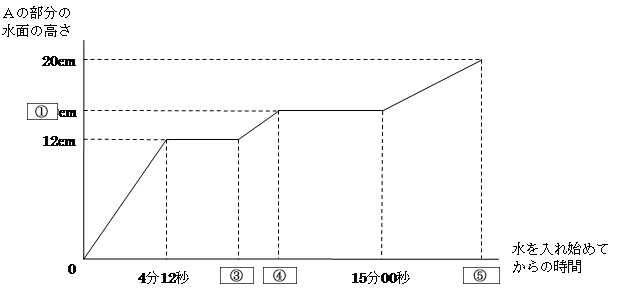
下のグラフは,水を入れ始めてからの時間とAの部分の水面の高さの関係を表しています。
解説
仕切り板のある水槽に水を入れる問題はよくありますが、円柱形の水槽を中心角で仕切っている問題はあまり多くないですね。
でも、底面積が中心角に比例するというだけで、基本的な考え方に違いはありませんから、分かりやすいように見慣れた形の図に書き換えてしまいましょう。
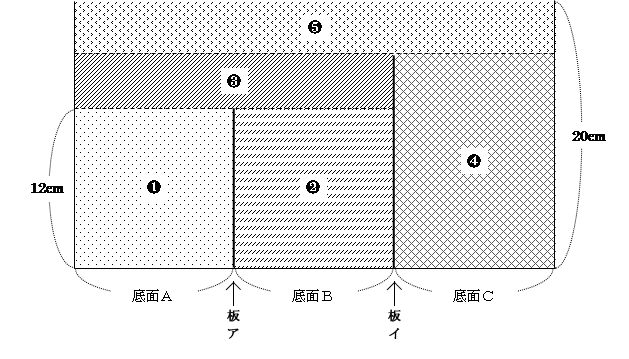
問題の図と、どのように関連しているか分かりますか? 水は、図の ❶→❷→❸→❹→❺の順に入っていくことになります。❶と❷の間にあるのが「仕切り板ア」,❷(❸)と❹の間にあるのが「仕切り板イ」ですね。このように簡略化することも、難問を解くための大切なポイントなのです。
さて、柱の体積は「底面積×高さ」ですから、この水槽の体積は10×10×3.14×20 で表されます。もちろん、この数字なら簡単に計算することもできますが、どうせ後からわり算をするので、ここではまだそのままにしておきましょう。 この水槽に、水を毎分314㎤の割合で入れていきますから、満水(❶+❷+❸+❹+❺)にするためには、
| 10×10×3.14×20 | = | 20(分)←⑤ | ||
| 314 |
かかります。
次に、仕切り板イの高さ( ➀ cm)まで水が満たされた(つまり、❶+❷+❸+❹の部分に水が入った)のは、与えられたグラフから15分00秒後と分かります。一定の割合で水が入っているのですから、入った水の体積は水を入れた時間に比例しますね。つまり、(❶+❷+❸+❹)と(❶+❷+❸+❹+❺)の体積比は、 15:20=3:4 となります。
そして、(❶+❷+❸+❹)と(❶+❷+❸+❹+❺)の差は❹の分だけですから、(❶+❷+❸+❹):❹=3:1 と直すことができます。
ここで、(❶+❷+❸+❹)と(❹の部分)を見比べると、底面積が等しい(A+B+C)ことに気がつきます。底面積が等しければ、その体積は高さ(深さ)に比例しますので、(❶+❷+❸+❹)と(❹の部分)の高さの比も3:1ですね。この比で水槽全体(❶+❷+❸+❹+❺)の高さ20cmを配分すれば、仕切り板イの高さ( ➀ cm)は、
| 20× | 3 | = | 15(cm)←➀ | |
| 3+1 |
と決まります。
徐々に空欄が埋まっていく感じ、何だかワクワクしますね (^^♪
ドンドン行きましょう!
❶の部分を見てください。与えられたグラフから、この部分を満たすのに要した時間は4分12秒です。水を入れる割合は毎分314㎠ですから、この部分の体積は、
| 314×4 | 12 | (㎤) | |
| 60 |
ですね。
そして、❶部分の高さは12cmですから、底面積(A)は
| 314×4 | 12 | ÷ | 12(㎠) | |
| 60 |
で求められます。
この面積と水槽全体の底面積(A+B+C)の比は、
| (314×4 | 12 | ÷12) | 12):(10×10×3.14) | |
| 60 |
……これを簡単にすると、7:20 となります。
実際にはおうぎ形の底面なので、この面積比は中心角の大きさの比でもあります。したがって、Aの部分の中心角は
| 314× | 7 | = | 126(度)← ② | |
| 20 |
と分かります。
また、底面Aと底面Bの面積比は、おうぎ形の中心角の比ですから、126:108=7:6 です。これは、❶部分と❷部分の体積比でもありますし、そこに水を満たすのにかかる時間の比でもあります。
❶部分に水を満たすのにかかった時間が
| 4分12秒(4 | 12 | 分= | 4.2分) | |
| 60 |
でしたから、 (❶+❷)に水を満たすためにかかる時間( ③ )は、
| 4.2× | 7+6 | = | 7.8(分) = 7(分)48(秒) ← ③ | |
| 7 |
です。
よし、ここまでくれば、あと一息!
(❶+❷)と(❶+❷+❸)の体積比は、同じ底面積(A+B)の部分ですから高さの比と等しくなります。したがって、(❶+❷):(❶+❷+❸)= 12:15 =4:5 です。
そして、体積比は、水を満たすのにかかる時間の比でもありますから、(❶+❷+❸)の部分に水を満たすのにかかる時間( ④ )は、
| 7 | 48 | × | 5 | = | 9 | 1 | (分)= | 9(分)45(秒) ← ④ | ||
| 60 | 4 | 4 |
と求められます。
比の扱いに慣れれば短時間でも解ける問題ですが、なかなか難しいですよね。さすがは女子御三家の一角というところでしょうか。
ところで……この問題が出題された翌年(2014年度)、開智中学校で次のような問題が出されました。あまりにも似ていて笑ってしまいますね。
最後に解答も載せておきますので、本問題の復習がてら、練習として解いてみてはいかがでしょうか。
平成26年度(2014年度)開智中(第1回) 大問4
図Ⅰのような,底面の円の半径が10cm,高さが20cmの円柱の形をした水そうと,3枚の長方形の仕切り板ア,イ,ウがあります。それぞれの仕切り板の高さは,12cm,15cm,20cmです。
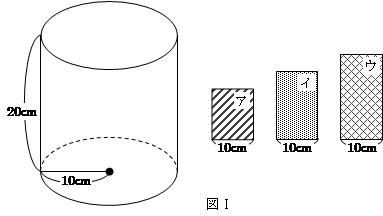
図Ⅱのように、仕切り板を底面に垂直にぴったりと入れて,A,B,Cの3つの部分に分けました。図Ⅲは,水そうを真上から見た様子です。ただし,水そうと仕切り板の厚みは考えないものとします。
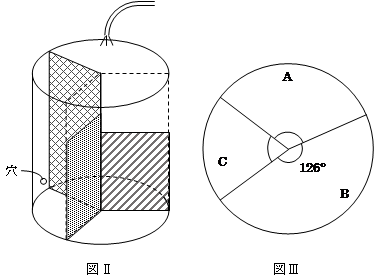
水をAの部分から毎分314㎤ずつ入れ始めました。しばらくして,仕切り板アをこえて水はBの部分に入り,さらにその後仕切り板イをこえてCの部分に水が入り,最後は水そうがいっぱいになりました。
ただし,Cの部分の側面には底面から高さが5cmのところに穴があいていて,水が毎分 え ㎤で円柱から出ていきます。
下のグラフは,水を入れ始めてからの時間とAの部分の底面から水面までの高さの関係を表しています。

このとき, あ , え にあてはまる数と, い , う , お にあてはまる時間を答えなさい。ただし,円周率は3.14とします。
解答
あ…15cm,い…8分24秒,う…10分30秒,え…78.5 ㎤,お…22分40秒
指導実例【理科】
平成24年度(2012年度)麻布中 大問3[抜粋] に挑戦してみましょう。
問題
問題)図1のように,長方形の先をとがらした図形Aと,同じ形をした2枚の長方形B,Cと,さらに同じ形をした3枚の長方形D,E,Fの3種類の図形を同じ厚紙で作りました。Aのとがったところを点Pとします。Aの上にBとCをはって図2のような物体を作りました。この物体を水平に支えてから点Pを棒の上にのせて,支えている手を静かに離(はな)すと,図3のように全体が水平のままつり合いました。以下の問いに答えなさい。

問1 長方形Dを図4のように図2の物体のAにはりつけました。この物体を水平に支えてから点Pを棒の先にのせて,支えている手を静かに離すと,この物体はどうなりますか。
問2 長方形Dを図4の物体から取り外し,図5のように長方形にEとFを,長方形BとCの先にはりつけました。このとき,のりしろは同じ幅(はば)にしました。問1と同じように,この物体を水平に支えてから点Pを棒の先にのせて,支えている手を静かに離すと,この物体はどうなりますか。
プラスチックでできた中空の球の1点に,目印のために小さな棒をはりつけました。ただし,棒の重さは無視できるものとします。
次の問3から問5の答えは,下の解答群のア~オからもっとも適当なものを選び,記号で答えなさい。同じものを何回選んでもかまいません。
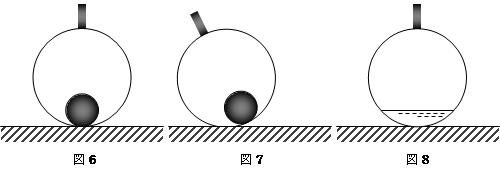
問3 図6のように,球の中で棒の真下になるところにおもりをはりつけました。図7のように棒を使って球をある角度まで傾(かたむ)けていったん止めてから,棒を静かに離しました。球はどうなりますか。
問4 図6のおもりを取り除き,図8のように水を少し入れました。問3と同じように球を傾けていったん止めてから,静かに離すと球はどうなりますか。
問5 問4の水を取り除き,図8のように蜂蜜(はちみつ)を入れました。 ① 問3と同じように球を傾けていったん止めてから,すぐに静かに離すと球はどうなりますか。 ② ①の蜂蜜を入れた球を図8の状態にもどしてから,問3と同じように球を傾けて,十分な時間がたった後に棒を静かに離しました。球はどうなりますか。
[解答群]
ア.傾いたままで止まる。
イ.さらに大きく傾くように動く。
ウ.すぐにもとへもどるように動く。
エ.しばらく傾いたままでその後もとへもどるように動く。
オ.方向が定まらず回転を始める。
~ 以下省略 ~
解説
ある程度以上の年齢の方なら、図1~5を見た途端に「やじろべえ」が頭に浮かんだのではないでしょうか?
そう、問1・問2の根底にあるものは、間違いなく「やじろべえ」なのです。
また、図6・図7を見た途端に「起き上がりこぼし(ダルマ)」が頭に浮かんだのではないでしょうか? これもご名答です。出題者は、明らかに昔のおもちゃを題材にして問題を作っていますね。
そして、それらのおもちゃに触れて育った大人にしてみれば、これらの問題は直感だけでも正答できる簡単な問題と言えます。
しかし、昔のおもちゃに触れた経験が少ないお子さんにとっては、大人なら簡単にわかる問2なども、意外な難問となるかもしれません。かといって、出題される確証もない昔の様々なおもちゃに、今から触れさせる時間を取るというのも現実的ではないでしょう。だから、仮に知らなくても、理論的に考えて答えを導き出せる力を身につけさせることが理想なのです。
さて、少し視点を変えてみましょう。この入試問題、本来は問8まで存在します。
問1~2は、「やじろべえ」をモチーフとした問題。
問3~5は、ダルマのような「起き上がりこぼし」をモチーフとした問題。
問6~8は、起き上がりこぼしの問題で考察したことを踏まえて、柱状の直方体の中に粘土や水や蜂蜜を入れて台の端からはみ出させる問題(何cmまでなら台から落ちずにはみ出させることができるかを問う設題)。
「昔のおもちゃ」という以外にも、この大問全体を貫く大きなテーマがあります。それは「重心の位置」です。
「やじろべえ」も「起き上がりこぼし」も、重心の位置が傾いた方向とは逆側にくることによって復元力を得て、もとに戻ろうとすることを利用したおもちゃなのです。
少し具体的に見てみましょう。
まずは図2の図形について考えます。
図3のように、点Pを棒の先にのせた状態で水平につり合ったのですから、この図形の重心は点Pであることがわかります。
ここに、図4のように長方形Dをはりつけたのですから、全体の重心の位置は、図Ⅰのように、長方形Dの重心の方向に移動することになります。
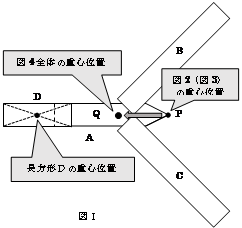
重心というのは、物体の重さが一点に集まっていると考えることができる点のことですから、図4の図形の重さは、左向きに移動した新しい重心位置Qにすべて集まっていると考えます。
この状態で点Pを棒の先にのせると、当然重心のある左側(長方形D側)に傾くことになりますし、棒から落ちることになります。
次に、図5のように2枚の長方形をはりつけます。同じ大きさの長方形を、同じのりしろで(つまり同じ距離の場所に)はりつけたのですから、この2枚の長方形を一つにまとめて考えると、その重心位置は2枚の長方形の重心のちょうど中点(M)となります。
そうすると、図Ⅱのように、図5全体の重心位置Rは、元々の重心位置PからMの方向に移動した位置にくることになります。この重心位置R(何もないところですが)にすべての重さが集まっていると考えられるので、重心Rに引っ張られてこの図形は点Pを中心に回転し、やがて図Ⅲのように重心Rが棒の中に入ったところで止まることになるのです。
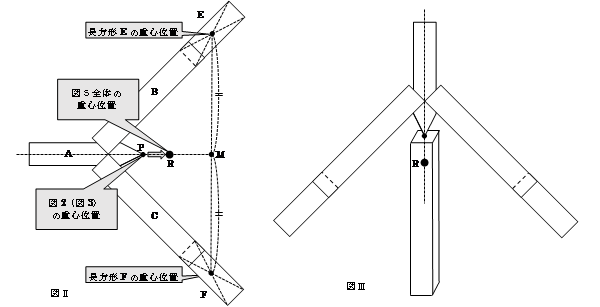
ところで……この問題とは関係ありませんが、この状態から、この図形を図Ⅳのように傾けてみると、重心Rの位置は、傾けた方向とは逆側に移動することがわかりますね。
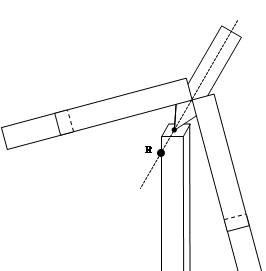
この重心が逆向きの力をかけてくれるために、手を離すと、この図形は元の状態(図Ⅲの状態)にもどろうとします。
もちろん、逆向きに傾けても同様のことが起こるので、ゆらゆらと揺れながらもバランスを取り、棒の先で落ちずにいるようになります。
これが「やじろべえ」が倒れない理由なのです。
問3以降の「起き上がりこぼし」の問題でも、ほぼ同様のことが起こります。
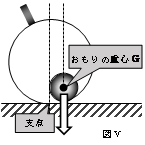
固定されたおもりの場合、問題の図7のように傾けると、おもりの重心Gは図Ⅴのように傾けた方向とは逆側に移動していることがわかりますね。この重心にかかる力が復元力となり、傾いた球をもとにもどそうとするのです。
ただし、中に入っているのが水の場合には、球を傾けたときに、水自体も球の中で移動してしますので、復元力がはたらかなくなります。棒の重さが無視できない場合には、上部につけた棒の重さの分だけ球全体は同じ向きに倒れ続けることになりますが、この問題では棒の重さは無視できるという条件がありますので、手を離したところで静止する結果になります。
一方、同じ液体でも、蜂蜜のように粘り気がある液体の場合には、水のようにすばやく移動しませんから、傾けてから手を離すまでの時間によって結果が違ってくるのです。
もちろん、すぐに手を離せば、蜂蜜の位置は固定されたおもりの場合と同じですから、復元力がはたらいてもとに戻ろうとします。
また、十分に時間がたってから手を離した場合には、蜂蜜が球の下の部分にたまるため復元力がはたらかず、水の場合と同様にその場で静止するのです。
さて、せっかくここまで学習したのですから、問題が解けただけで満足してしまうのはもったいないですね。
実は、重心位置の移動によって復元力を作り、倒れないようにするという仕組みは、船などにも使われているのです。
下の図は、船を正面から見た模式図です。
通常、船は、下の図のように、低い位置に重心がくるように設計されています。
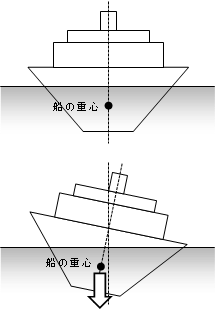
そのため、波や風で船体が揺れても、傾いた向きとは逆側に重心が移動し、船の傾きをもとにもどそうとする復元力がはたらくのです。
2015年に中国で起きた船の転覆事故は記憶に新しいところですが、川は海に比べて底が浅いために、船の水面下の部分がもともと薄く造られています。それなのに、船の上部に客室を作るなどの改造をほどこしていたようですから、船全体の重心の位置が高くなり、十分な復元力を得られなくなっていたのかもしれません。

