みなさん、こんにちは。
受験ドクター算数科の江田です。

梅雨の季節ですね。

ちなみに、昨年の関東の梅雨明けは
例年よりもやや遅く、7月末でした。

そして、梅雨が明けたら
いよいよ本格的な夏到来！！

受験生にとっては
中学受験最大の山場ともいえる
夏休みを控えるこの時期。

保護者の皆様も、
しっかり体調管理をなさって
お子様を支えてあげてくださいね。

さて、今回は
前回お話した「平方数」の続きです。

前回の「平方数の和って？①」はこちらへ！
/koushi_blog/edam/20170512.html//

 

前回、
神戸女学院中等部
の問題をご紹介しました。

1×1＋2×2＋3×3＋4×4＋5×5

という計算において、
正方形を並べた図を活用し、

最終的には

1×1＋2×2＋3×3＋・・・・・・＋49×49＋50×50

という計算も、
図形の面積から考えることができました。

今回は、
同じ「平方数の和」を
別の図から考えていきます。

では、さっそくいってみましょう！

 

下の図の正三角形(ア)の中に入っている数の和を考えます。

1が1個、2が2個、3が3個、・・・・・・、6が6個ですから

1×1＋2×2＋3×3＋4×4＋5×5＋6×6

の計算をすることになりますね。
そう、「平方数の和」です。

これを、次のように考えてみましょう。

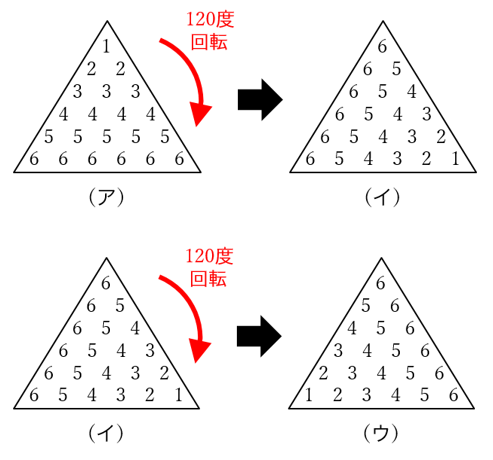
正三角形(ア) を時計回りに120度回転させたものと、
さらに120度回転させたものを用意し、
それぞれを正三角形(イ)と正三角形(ウ)とします。

そして、(ア)から(ウ)の3枚を重ねて
それぞれの場所にある数の和を考えてみると…

(エ)のように、どの場所の和も13になります。
(たとえば、＿の部分は3＋4＋6＝13となります。)

だいぶ見えてきましたね…

その通りです。
(エ)の中の数の和を求めて3等分すれば
(ア)の中の数の和になりますね。

さあ、もう一息です！

(エ)の中に、数は何個あるのでしょう。

上から順に、段ごとに個数をたしていけば

1＋2＋3＋4＋5＋6＝21(個)

とわかります。
したがって、(エ)の中の数の和は

13×21＝273

と求められ、(ア)の中の数の和は

273÷3＝91

とわかるのです。
では、この方法を利用して

1×1＋2×2＋3×3＋・・・・・・＋99×99＋100×100

を計算しましょう。

 

そうです。
先ほどと同様に正三角形を用意し、
120度ずつ回転した図をイメージしてください。

3枚重ねると、どの場所も和は

1＋100＋100＝201

で、その個数は

1＋2＋3＋・・・・・・＋99＋100＝(1＋100)×100÷2
＝5050(個)

ですね。
よって、求める答えは

201×5050÷3＝338350

です！

いかがでしたか。
高校数学で学ぶ

という公式を知らなくても、
算数の世界で「平方数の和」は
求められるのです。

 

もちろん、
今回ご紹介した考え方を
暗記する必要は全くありません。

 

今回の話題は、
法政大学第二中学校で出題されたものを
もとにしましたが、
前回の神戸女学院中等部と同じように、
「その場で考える力」
を試されているのです。

 

難関校のみならず、
近年は、多くの学校でこのような
「新出問題(に見える問題)を、その場でじっくり考えさせる」
タイプの出題傾向が見られます。

このような問題に対応するために
「普段から物事を深く考える」
姿勢を大切にしましょう。

6年生はこれから先の問題演習において、
一見難しそうな問題に出くわしても、
簡単にあきらめず、
一歩踏み込んで考えてみてください。

また、4年生、5年生のお子様は
これからいろいろな公式を学ぶ際に
“ただ覚える”のではなく、
「なんでこの公式になるんだろう」と疑問を持ち、
自分で調べ、他人に説明できるようになると
考える力がつくだけではなく、「算数のおもしろさ」を
感じられるようになるかも知れませんよ♪^^

今回はここまで。

みなさん、これからやってくる本格的な暑さに負けず
頑張りましょう！

ではまた。