みなさん、こんにちは。
受験ドクター　理科・算数担当のT.H.です。

今回は入試頻出の化学計算の中でも、中和の計算。
特に苦手とする人の多い塩酸に水酸化ナトリウム水溶液を加えていく問題を扱ってみます。

問　　塩酸50㎤に様々な量の水酸化ナトリウム水溶液を加え、A～Gのビーカーをつくりました。できた水溶液を蒸発させて残った固体の重さを量り、表にしました。

塩酸50㎤を完全に中和させるのに必要な水酸化ナトリウム水溶液の量を求めなさい。

なぜこのパターンを苦手とする人が多いのか。
理由は残った固体にあります。

塩酸を加えていく実験であれば、中和したあとにいくら塩酸を加えても固体はできませんが、
水酸化ナトリウム水溶液を加えると、中和したあとも水酸化ナトリウムの固体が残ってしまいます。

グラフにするとこのような形になります。
グラフが折れ曲がった点が完全中和をした場所です。
完全中和したということは塩酸が全て使われて無くなったということなので、その後は水酸化ナトリウム水溶液を追加した分だけ、水酸化ナトリウムの固体が増えていくことになります。
右上図のように中和でできた食塩と、水酸化ナトリウムを区別するとわかりやすくなります。
この2種類の固体が混ざっていることによって、理解しづらくなってしまいます。

ではこの問題はどう解くかというと、

まずはどんな問題でも同じ作業です。
表が描かれていたら必ずとなりとの差を書き込み、変化の規則を見つけましょう。

固体の増え方が、＋1.2g　、＋1.1g　、＋0.8g　の3段階になっています。
グラフにすると、下の赤線のような形になります。

このように2か所で折れ曲がっているグラフは、ありえません。
＋1.1gの部分を使ってしまうと誤ったグラフになるので、計算も間違えてしまいます。

このような問題の解き方を2種類ご紹介します。

① つるかめ算で解く　（おすすめ度 ★★☆）

理科計算もここまでくると、算数の問題と解き方が変わらなくなってきます。
算数の分野でこの問題に一番近いのは、速さが途中で変わる問題です。
速さが変わった点を見つけるためには、2つの速さと合計時間、合計の道のりが必要となります。

つまり
2つの「単位量あたりの増加量」と、2つの「合計」がわかっている場合はつるかめ算が使えます。

ビーカーA～Gの範囲で考えると、水酸化ナトリウム水溶液1㎤あたりの固体の増加量は、
前半→0.12ｇ、　後半→0.08g
水酸化ナトリウム水溶液の合計60㎤、　できた固体の合計6.3g
「単位量当たり」と「合計」が2つずつあるので、つるかめ算が使えます。

すべて0.08gずつ増加したとすると、0.08×60＝4.8gの固体ができるはず。
実際の固体の合計とは6.3－4.8＝1.5gの差ができます。
ここで水ナト1㎤あたりの差は0.12－0.08＝0.04gあるので、
1.5 ÷ 0.04 ＝ 37.5㎤
1.2gずつ増えていたのは水ナトが37.5㎤までなので、これが答えとなります。

② 逆比で解く　（おすすめ度 ★★★）

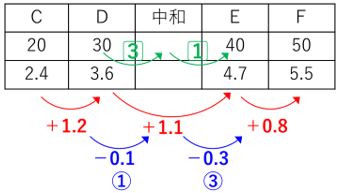
下表の青字部分のように先ほど書き込んだ重さの増加量に加えて、さらにその差も書き込みます。
ＤとＥのあいだで完全中和しているので、その前後だけで大丈夫です。

増加量の差は0.1ｇと0.3ｇ、　比にすると1：3となっています。
すると下表のように完全中和したときの水酸化ナトリウムの量はＤとＥのあいだで
先ほどの逆比である3：1の点となります。

この理由は平均の考え方で説明できます。

Ｄのところまでは1.2gずつ、Ｅのところでは0.8gずつ増えています。
その変化の境目（完全中和点）がDからEまでの10㎤のどこかに
あすはずなので、面積図を描くとue 図のようになります。
図より、10㎤を3：1に分ける点で完全中和していることがわかる
ので、増加量の差の逆比で求められることがわかります。
したがって、完全中和点はDから
10㎤ × = 7.5㎤すすんだ場所なので、
30 ＋ 7.5 ＝ 37.5㎤

時間効率を考えると、逆比で解くことに慣れたほうが入試に有利です。
苦戦した問題をこの解法で解き直して、本番で使うためのトレーニングをしておきましょう。