皆さんこんにちは。
受験Dr.講師の勝山利信です。

前回は「音の数値化と視覚化」をテーマに、音についての理解を深めるお話をしました。
今回は引き続き音をテーマに、より実践的な問題の考え方についてお話します。

モノコードの条件を変えた場合に、音の高さがどのように変化するか数値を用いて考えてみましょう。

まずはおさらいですが、音の高さを決めるものは何でしょうか？
少し幅の広い聞き方ですが、直接影響するのは振動数です。
そして、振動数を変化させる要素がいくつかあることがポイントになります！

では、具体的にどのように与えられた条件をとらえていけば良いのか見ていきましょう。

 

条件と結果の間を埋める＝理解が深まる

さて私の授業を受けた生徒も含めてですが、音の学習をした後にノートにどのようなことが残っている可能性が高いかというと・・・

というような、音の高さに関するまとめです。
理科の知識事項として身につけておきたい重要なことですが、これを覚えたからと言ってすぐに数値的な処理がスルスルとできるようになるわけではありません。算数の学習と同じで、理解したうえで具体的な問題でトレーニングすることが大切です。

では、先ほどまとめたことについてどれだけ理解しているでしょうか？
一つの判断基準としては、数値処理をする問題の解答で大小関係をまちがえないことです。
計算ミスによる場合もありますが、本当に理解している場合は、答えるべき数値はこの数値よりも大きくなるはず、または小さくなるはずという大小関係をまちがえなくなります。

例えば、弦の長さだけを変化させた２つの音を比べたときに、弦が長い方の振動数が大きくなっているということが起こるのであれば、まだ理解が甘い部分が残っているのでしょう。

①強く張る
弦はそもそもぴんと張って音源にします。その張り方が強いと、もとの位置に戻ろうとする力が強くなり、速く振動することになるので振動数が増え音は高くなります。
②短くする・③細くする
弦は非常に軽いのですが重さがないわけではありません。短くしたり細くしたりすれば、振動する部分が軽くなり、同じ力で弦を張っているとき、もとの位置に戻る力が少なくてすむので、速く振動し振動数が増えます。

このように理由があって振動数が増えるので、条件と結果だけでなく簡単な理由も一緒に確認し、知識を定着しやすくしましょう。

 

現象を数値化してとらえる

先ほど確認した知識事項は実験を通して分かったことです。
テストの問題でも実験データを正しく利用して考えることができるか問われる問題がよく出題されます。

それでは、与えられた数値のどこをどのようにとらえて考えていけば良いのか確認していきましょう！

～例題～
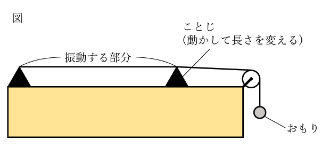
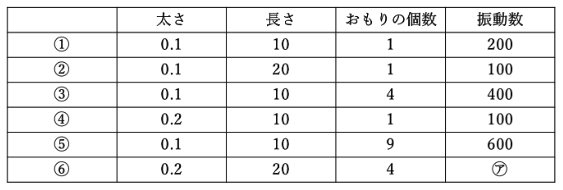
図のようなモノコードを使って、音の性質について調べました。表は、弦の太さ、長さ、弦につるすおもりの個数を変えて、弦の中央を同じ力ではじいたときに出る音の１秒間の振動数を調べたものです。表の㋐にあてはまる数値を答えなさい。

さて、どこから考えていけば良いでしょうか？
問いに対する答えは、㋐にあてはまる数値を答えるわけですが、苦手な人ほど⑥の条件から考え始めてしまいます。

まずは、条件である太さ、長さ、おもりの個数が振動数という結果をどのように変化させているのか、関係性を読み取ることから始めましょう。

①と②⇒長さが２倍になると振動数は倍になる（反比例）

①と④⇒太さが２倍になると振動数は倍になる（反比例）

知識事項を先に確認した通り、長くなったり太くなったりすると振動する部分が重たくなり振動するのが遅くなるので、反比例して振動数が小さくなることが分かります。

①と③と⑤⇒おもりの個数が４(２×２)倍、９(３×３)倍になると、振動数は２倍、３倍になる

物理の条件と結果の関係を考えると、平方数（２個の同じ整数をかけた数）が関係してくることがしばしばあります。おもりの個数が増えて弦を張る力が強くなると振動数は大きくなりますが、単純に比例はしていないので注意しましょう。

実際に関係性を確かめる実験を行う場合は、もっと多くのパターンの実験を行い比較します。
問題で出題される場合は、事前に学習してきたことが前提なので与えられる実験パターンは少なくなります。
与えられたデータに基づいて、関係性を正しく読み取りましょう。

関係性が読み取れたので、ここで初めて⑥を見ます。
㋐にあてはまる数値を考えるために③と比較してみましょう。

それぞれの条件が結果とどのように関係しているのか確認しているので、①～⑤のどの実験結果と比較しても計算することはできます。③と⑥はおもりの個数は同じなので、この条件は振動数の変化に影響しません。おもりと振動数の関係には平方数が関係するので、計算ミスを極力防ぎたいのであれば、今回は③との比較がベストです。平方数の計算をしなければ解答できないパターンの問題もあるので、そのようなパターンのトレーニングは問題集などを使って行いましょう。

先ほど確認したように、太さと長さに反比例するため、倍の振動数になります。
よって、㋐にあてはまる数値は③の振動数の400をもとにして、
400×＝100　と、考えることができます。

 

今回はモノコードと音の高さの関係について詳しくお話しましたが、化学でも同様に関係性を読み取ってから倍率や比率を使って計算を進める反応量に関する問題はよく出題されます。話題は異なりますが、根本的な考え方は同じですので、取り組んでみると良いでしょう。

目指せ数値処理力UP！
それでは、またお会いしましょう！