皆さんこんにちは。
受験Dr.講師の勝山利信です。

前回に引き続き「ばねの伸び方」についてお話します。
基本的なばねの性質のとらえ方については、是非前回のブログを参考にしてください。
今回は複数のばねをつないだ場合について考えていきます。

組み合わせ方で難易度が大きく変わる！

ばねの基本性質は、かかる力の大きさ（おもりの重さ）に比例して伸びるというシンプルなものですが、それを組み合わせることで複雑な問題も出題できます。

大きく分けると、「直列つなぎ」と「並列つなぎ」の２つの組み合わせ方があります。
直列や並列という言葉は電流に関する学習でも登場します。
意味は同じで、直列つなぎは（図１）のようにばねが一直線につながっているもの、並列つなぎは（図２）のように２ヶ所以上の位置に分けてばねをつなぐ様子を指します。

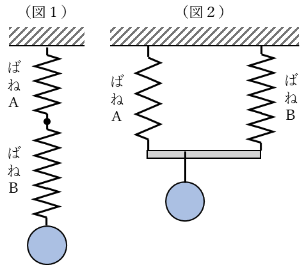
応用的なばねの問題に取り組むときは、直列つなぎと並列つなぎのどちらのパターンか、まず確認しましょう！今回は直列つなぎのパターンについて考えます。

直列つなぎのとらえ方

直列つなぎでばねをつないでいる場合は、ばねやおもりにかかっている力の大きさを順に考えていきましょう！
原則、下向きにおもりの重さがばねにかかり、その重さをばねが支えるので、下から見ていきます。
例えば（図３）のようにつないでいるのであれば、おもりをばねBが支え、ばねBをばねAが支え、ばねAを天井が支えているというように、力をお互いにかけ合うことになります。天井は柱が支えています。

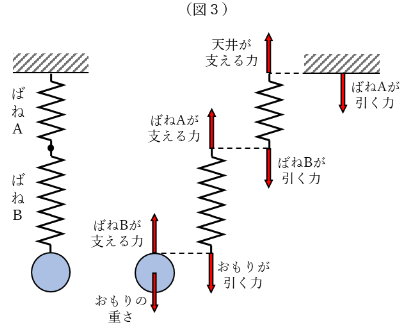
この場合は、おもりの重さが引き継がれていくことで、ばねAとばねBには同じ大きさの力がかかり、それぞれの伸び方に従って、ばねが伸びます。「ばねBにおもりをつるしているので、ばねAには力がはたらいていない。」は誤った考え方なので注意しましょう。

それでは、次のような場合はどのように考えれば良いでしょうか？

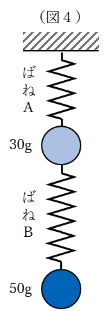
ばねAとばねBの間にさらにおもりをつるしました。
２つのばねは一直線につながっているので、直列つなぎの一種と考えられます。
この様子を見ると、様々なとらえ方をしてしまいどのように考えれば良いのか迷ってしまうこともあります。
そのようなときこそ、原則に従って考えましょう！
（図５）のように力のかかり方を確認します。

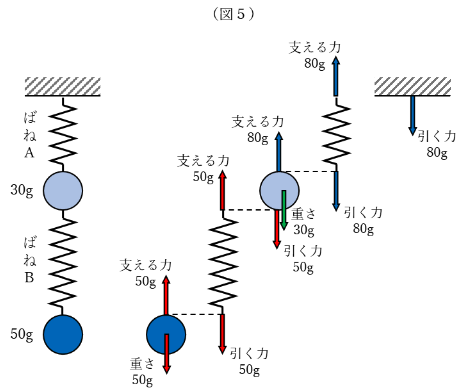
やや情報量の多い図ですが、下から順におもりやばねにかかる力の様子を確認しましょう！
ばねBは50gのおもりを支えれば良いので、50gの力がかかってその分伸びます。
ばねAは引き継がれてきた50gの力と、30gのおもりを支える力も必要になり、合計80gの力がかかっています。

このように、直列つなぎのばねは下から順に力のかかり方の様子を確認していくと、伸び方やばねの長さを考えることができるようになります。

家庭学習とテスト中の取り組み方

テスト中に一つ一つの部品をバラバラに書いて丁寧に力のかかり方を確認していると、時間がかかりすぎてしまうでしょう。今回の図の様子を参考にして力のかかり方について理解を深めるため学習を家庭学習で行い、テスト中は部品の近くに数値だけ書きこむなど工夫し、問題を解くのにかかる時間を短くできるように取り組みましょう。

次回は、ばねの並列つなぎについてお話します。

目指せ理解力UP！
それでは、またお会いしましょう！