皆さんこんにちは。
受験Dr.講師の勝山利信です。

今回のテーマは「天体の大きさや距離」についてです。
地学の中でも天体の分野は宇宙規模で起こる現象について考えるので、扱われる数値が最も大きくなる分野です。数値が大きすぎるのでイメージがしにくく、考える際に使用する図も実際の大きさのバランスで描くと大きくなりすぎたり小さくなりすぎたりするので、理論が確認できる程度にバランスを変更して表した模式図（モデル）を使うことがほとんどです。

また、テキストなどに掲載されている天体に関する資料を見ると、情報量が多すぎて「これを全部覚えなくてはいけないのか！？」と困ることもあります。もちろん、入試では細かい知識を問われることもあるので、知識を増やしておくことに越したことはありませんが、その１問に答えるために暗記に費やす時間がかかりすぎるので効率は良いとはいえません。そこで、考え方の土台になる事柄やそれを覚えておくべき理由とともに優先して覚えるようにしましょう。

押さえるべき数値は押さえる！

今回は規模が大きすぎる話題ですが、私たちはそもそも「長さ」を普段からどのようにとらえているのでしょうか？
長さを考えるときに、単位として「ｍ(メートル)」を用いることが一般的です。
生活の中でも使用するので、１ｍや１ｃｍという長さがどのくらいの大きさであるか感覚的に分かっている人も多いと思います。

ここで大事なことは、１ｍという長さを決めるときに地球を基準に定めたということです。
調べてみると、現在では一度定めた１ｍの長さをより厳密にするために新たな基準が設けられていますが、もともとは地球の大きさから１ｍという長さを次のように定めました。

「 赤道から北極までの子午線(弧)の長さの1000万分の１の大きさを１ｍとする 」

簡単に言うと、「 地球の円周は4000万ｍ＝４万km 」だということです。

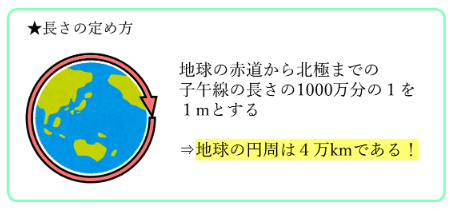
その他の長さもmやkmを用いて考えるわけですから、地球の円周が4万kmであることは、長さを考える上での根本原理です！重要な基礎知識としてしっかりと確認しておきましょう。

さて、地球の円周が4万ｋｍなのであれば、直径はどのくらいの大きさと言えるでしょうか？
ここでは地球をほぼ球体ととらえて、計算してみましょう。
円周率を3.14として（簡易的に約３でも大丈夫！）計算して見ると、

（地球の直径）×3.14＝4万km より　(地球の直径)＝4万km÷3.14≒12700(km)　と計算できます。

実際の大きさは約12756kmとすることが一般的で、サイズ感として認識する数値はおよそ1万3000kmで問題ありません。

この「問題ありません」というのは、テストで問われたときにこの程度のサイズ感が持てていれば十分に問題は解けるということです。

次に、地球に身近な星として太陽や月に関する問題もよく出題されるので、大きさを押さえておきましょう。
太陽の直径は約139万2700km（約140万km）、月の直径は約3475km(約3500km)です。
また、地球からの距離は、太陽が約1億4960万km(約1億5000万km)で、月が約38万4400km(約38万km)です。
これらの数値を使って解く問題なのであれば条件として与えられます。
他の条件からこれらの数値を計算する場合もあり、計算結果は知識として知っている数値に近い値になるはずです。計算間違え、特に小数点の位置がずれてしまったときなどに、上から２桁の概数程度のサイズ感で覚えておけば間違いに気がつくきっかけになります。

具体的な数値以上に倍率でとらえて考えることも多いので、確認しておきましょう！

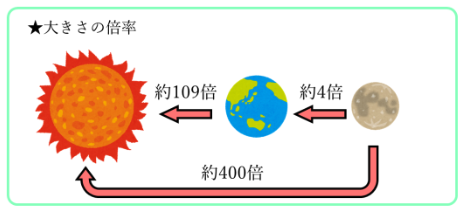
先ほどの直径の数値を使って倍率を計算して見ると、上の図のようになります。
このことは、太陽の直径は月のおよそ400倍の大きさですが、地球からの距離もおよそ400倍離れているため、地球から見える太陽と月の大きさはほぼ同じ大きさとなり、日食のときにぴったりと重なることで皆既日食や金環日食が起こることの理解に重要な数値になります。

受験勉強としての学習

学習するときは、その内容に興味関心を持って自ら学ぶことが理想的です。しかし、受験のための学習は正に「勉強（いやなことでも我慢する）」であることも多く、苦手なことも学ぶ必要があります。目標を下げるのではなく、目標に到達するまでのスモールステップを踏んだり、今回のように負担をできる限り減らしたりと、工夫しながら取り組みましょう！

目指せ知識定着力UP！
それでは、またお会いしましょう！