こんにちは、受験Dr.の咲山です。

始まる前は長く感じる夏休みも、終わってしまえばあっという間だったかと思います。
今回は夏の昆虫の代表、「セミ」がテーマです。

皆さんは、素数ゼミを御存じでしょうか。
素数は算数でも出てくる「1とその数の2つのみ約数を持つ数」
2, 3, 5, 7, 11, 13, 17, 19・・・
この数にまつわる昆虫の「セミ」であることから、素数ゼミと呼ばれます。

日本にはおらず、北米固有のこのセミですが、現在生き残っている種は13年周期のセミと17年周期のセミであり、今年はその2種類が同時に大量発生する年でした。その数は世界の人口をゆうに超え、なんと１兆匹。

文字通り、けた外れの大量発生ですが、1803年、次の周期は2245年と、大量発生する周期は221年おき。
なぜわざわざ素数のような、計算では扱いづらい周期のセミが存在するのでしょうか。

今回は実際に過去に入試問題として使われたものを通して、
今年の時事問題としてテーマにもなる素数ゼミを知ってもらえたらと思います。

関西第一中学校　2019年　大問5（一部抜粋）

太郎君はインターネットで、「アメリカには13年ごと、17年ごとに大発生するセミが存在し、学者は天敵に食べつくされることや、近い種類のセミと交配することをさけることで、子孫をより多く残せるのではないかと推測している」という周期セミのニュースを見つけ、なぜ13、17という数字だけしかいないのか疑問に思い、もし12年、13年、15年、17年、18年周期ごとに大発生するセミがいると仮定したらどうなるか考え、自由研究で発表しました。次の空らん①～⑤に当てはまる数字を、⑥にあてはまることばを答えなさい。

12年周期セミと15年周期セミが今年同時に大発生した場合、次に同時に発生するのは60年後になると考えました。同様に考えてまとめた結果が下の表です。

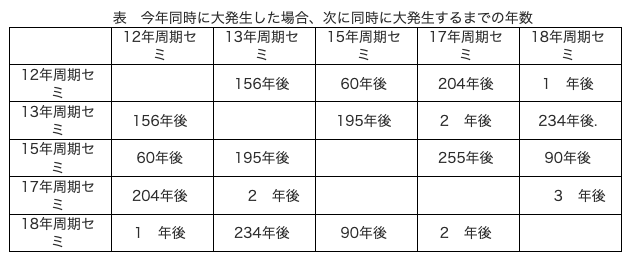
この表から④年周期セミと⑤年周期セミがもっとも大発生が同時に起こりにくいことが分かりましたが、⑤年周期セミは他の周期セミと大発生が同時に起こりやすいため、その種類のセミと交配しやすくなり、その結果共に滅亡していったのではないかと考えました。そのため、13と17という「2以上の整数で、その数と1以外に割り切れる数を持たない数」すなわち⑥の周期を持つセミが生き残ったのではないかと考えました。

～解説～
１～３は対応する2つの周期の最小公倍数を取ればよいです。
①36　　　（12と18の最小公倍数）
②221　　（13と17の最小公倍数）
③306　　（17と18の最小公倍数）

表の数値より、周期が重ならないのが、③に当てはめた、306です。306年おきの周期であれば、17年と18年の周期のセミ同士では交配を避けられます。しかし、18年周期のセミは12年周期と36年ごとに、15周期のセミと90年ごとに周期が重なってしまいます。他の数と約数を持つ素数以外の数（合成数）の周期のセミは、他の周期のセミと周期が被りやすくなります。

問題文では言及されていませんが、別の周期のセミが交配した場合（周期の違うセミは、ヒトでいう人種のようなもので、交配自体は可能です。）、子の代のセミの周期がずれることが確認されています。周期のずれたセミは交配相手を見つけることが難しくなるため、徐々に数を減らします。
こうして、周期が重なりやすい合成数のセミは数を減らし、現在は素数が周期のセミのみが残りました。

④17
⑤18
⑥素数

周期と素数という点が、算数ではあまり見られない組み合わせですが、
「素数」ということが逆に生存競争で有利にはたらき、生き残ることが出来た、ということです。

ちなみにこの素数ゼミの仕組みを解き明かしたのは、日本の大学の科学者です。注
生き物に限らず、様々な現象に対して、
「なぜ、どうして」といった疑問を持つきっかけとなってもらえたら幸いです。

以上です。次回も今年の理科の時事問題を紹介します。

参考：
注)　　吉村　仁　「素数ゼミの謎」，文藝春秋，2005年7月