皆さま、こんにちは！

前回、前々回と、ご家庭からの「優先すべき科目は？」という、よくあるご相談についてご説明しました。
今回は、その第３弾です。
中学受験で優先すべき科目は算数で、理由は入試本番で圧倒的に差がつく科目だからです。
前回も書いたように、考えられる原因は３つあります。
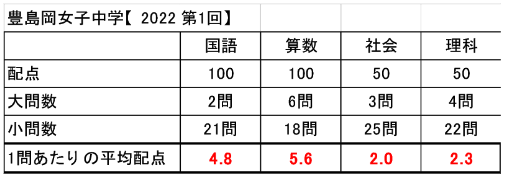
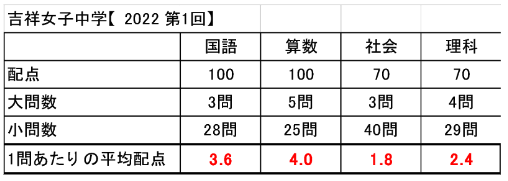
①問題数が少なく、1問あたりの配点が大きい
➁小問ごとのつながりが強く、続けて失点するリスクが高い
③他科目に比べて特殊性があり、専門的なトレーニングが必要
前回は、①について、データを見ながらご説明しました。
詳しくは、12/15のブログをお読みください。

 

算数は小問ごとのつながりが強い科目

今回は理由の②について、データをもとに考えてみます。
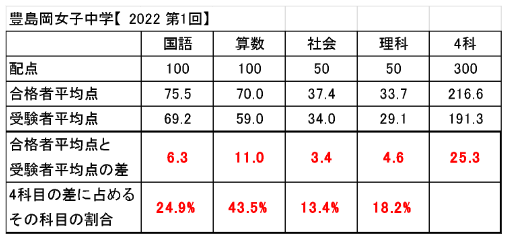
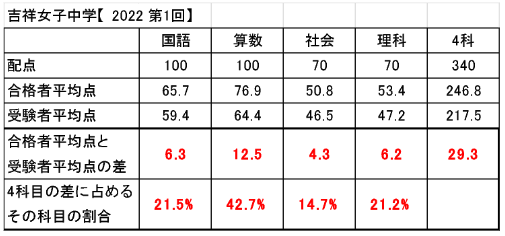
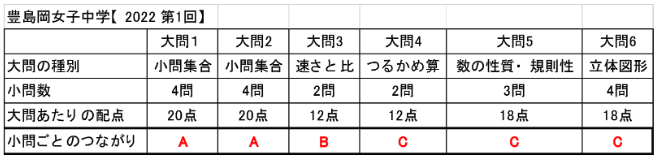
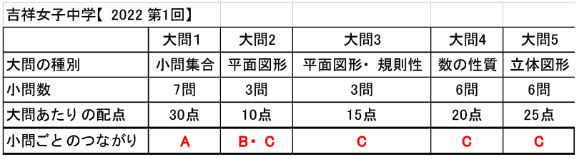
まずは、前回紹介した、女子中学３校のうち、豊島岡女子と吉祥女子のデータをもう一度見てください。

 

 

前回は、算数で差がつきやすくなる理由のひとつが、１問あたりの配点の大きさにあるということを説明しました。
しかし、よく数字を見てみると、この２校については、算数と国語の配点にそこまで大きな差はありません。
だとすると、なぜ算数だけここまでの差がつくのか、配点の問題だけでは説明がつきません。
それとは別の原因も絡んでいるはずです。
そこで考えられるのが、算数は小問ごとのつながりが強く、続けて失点するリスクが高いということなのです。

 

どの科目もそうですが、いくつかの大問のなかに、いくつかの小問が含まれているという形で出題されます。
このとき、その大問の（１）が解けないと、それ以降の小問が解けないということがどの程度ありうるでしょうか？
国語や理科、社会なら、そういったことはまず起こりません。
たとえば、（１）の用語を書けなかったからといって、（２）の選択肢問題を解けないということはないです。

 

ところが、算数はこういった事態が容易に起こります。
（１）で求めた数値を使って、（２）以降の問題を解くというのはわりと当たり前です。
ですから、（１）がそもそも解けないと、その大問は一切解けないということになります。
そうすると、その大問はまるまる０点です。
ひとつの小問が５点の配点だとしても、大問としては１５点～２０点くらいの配点になります。
（１）が解けないということは、５点の失点ではなく、１５点～２０点の失点を意味するということです。

 

算数の大問を３タイプに分類してみる

ここで、先ほど挙げた２つの学校について、小問同士のつながりがどの程度あるのかを分析してみましょう。
大問を以下の３タイプに分類してみます。
Aタイプ　小問ごとのつながりが一切ない
Bタイプ　前の小問で求めた数値が、それ以降の小問を解く際に必要になる
Cタイプ　前の小問で考えたことをさらに応用して、より複雑なことを考える

 

Aタイプは、計算問題や小問集合などで、入試問題の前半に多いです。
このタイプであれば、（１）が解けなかったとしても、それ以降の小問にはまったく影響がないです。
Bタイプは、先ほども説明した（１）が解けないとそれ以降の小問はまったく解きようがないというものです。
速さの問題などはこのパターンになることが多く、一番大量失点する危険があります。
Cタイプは、小問ごとに直接的なつながりはないものの、（１）の解法が次の問題の大きなヒントになっています。
独立して問題を解くことはできますが、（１）が解けないと（２）以降を解くことは実際には難しいです。
図形や規則性の問題などがこのパターンになることが多いです。
Bタイプは直接的なつながり、Cタイプは間接的なつながり、と考えてください。
いずれにしても、Bタイプ、Cタイプともに、大問丸ごとの失点のリスクが高いです。

 

では、実際に先ほどの２校の問題を、大問ごとにこの３タイプに分類してみます。
以下の表を見てください。

 

 

いかがでしょうか？
ほとんどの大問がＢかＣのタイプになっています。
完全に独立している小問が並ぶのは、序盤の数問しかないということになります。
ただし、数問とはいえ、ここに３０点～４０点の配点があるということもポイントです。
このような出題形式の場合、とにかく序盤の簡単な問題をミスなどで落とさないということが重要になります。
その上で、後半の大問については、すべて解けなくて良いので、解けそうなものを拾うということを目指します。
特にＣタイプの場合、後半に行けば行くほど難しくなります。
（１）が解けたからといって、（２）以降が解けるかどうかはまったくわかりません。
問題によっては、捨てるという判断も大切になります。
この「拾う」「捨てる」という感覚も、おそらく算数にしかないもので、これも科目的な特殊性になります。
ということで、算数で差がつきやすいもうひとつの理由が、おわかりいただけたでしょうか？

 

国語や理科でも同様のことは起こり得る

同様のことが他の科目ではまったく起こらないかというと、そんなことはありません。
近いことがあり得るのが国語です。
特に、素材文を誤読してしまったときは、選択肢問題をことごとく間違えるということが起こります。
大問５０点の配点に対して、１０点くらいしか取れていないという場合は、素材文の誤読を疑ってみてください。
算数の次に差がつきやすいのが国語である理由は、このあたりに原因があると思います。

 

また、もうひとつ同様のことが起こり得るのは、理科の物理計算・化学計算の問題です。
特に、物理分野の力学の問題などは、前の小問の数値を利用して、次の問題を解くことが非常に多いです。
基本的な原理・原則を知っていれば、それ以上に特別な知識が必要ないのも力学の特徴です。
原理・原則に沿って正しく考えていれば、必ず答えにたどり着けます。
極論ですが、ちゃんとわかっていれば満点が狙えますが、わかっていないと０点があり得ます。
ですから、力学は非常に重要で、ここで大きく得点差がつく可能性があります。

 

ということで、算数や、国語の読解問題、理科の一部の問題は大量失点のリスクをはらんでいます。
ですから、ここに学習量を大きく割いていかなくてはいけないということです。
その中でも算数は、日常的にはなじみがない、特殊な解法やテクニックも必要になってきます。
算数で差がつきやすい３つ目の理由がここにあります。
これについては、次回のブログで考えてみます。
では、また次回お会いしましょう！