皆さま、こんにちは！

ご家庭からのよくあるお悩みについて、回答してみようという企画の第３弾です。
「やってもやっても伸びないのですが？」という、お悩みについて考えています。
前回は、１回目のブログで挙げた４つのチェックポイント
①取り組んでいるトレーニングの意味や理屈を言葉で説明できるか？
②取り組んでいるトレーニングはいまの実力や改善点に適したトレーニングか？
③取り組んでいるトレーニングの量やかける時間は適切か？
④取り組んでいるトレーニングが応用的な場合は基礎となることの理解は十分か？
このうちの、④について、私が最近何度か出くわした事例についてご説明しました。
わり算のイメージという基本的なことについても、実はわかっていない可能性があるということでした。
今回は、なぜそういうことになってしまうのか、その原因について考えてみます。

前回のおさらい

まず、前回の内容を軽くおさらいします。
わり算という計算にどういうイメージを持っているか？
これについては、同じ計算式でも、実は２つのイメージがあり得ます、ということをご説明しました。
たとえば、１５÷３＝５という計算がやっていることは、以下のような２つのイメージが考えられます。

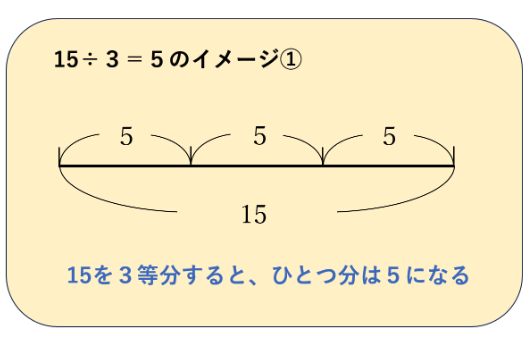
こちらは、１５という全体の大きさを、５ずつに３等分しているイメージです。
もうひとつのイメージはこちらです。

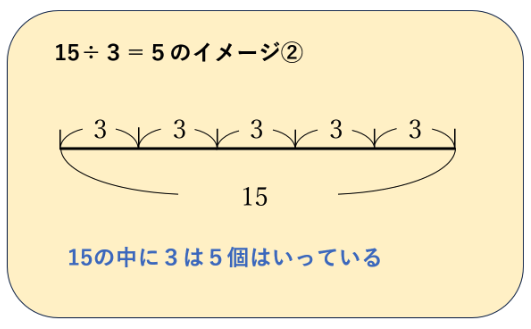
こちらは、１５という全体の大きさのなかに、３が５つ入っているというイメージです。
前回詳しくご説明したように、この２つのイメージはどちらも間違っていないです。
そして、問題によってこの２つのイメージはどちらも必要になります。
ところが、このイメージが片方しかわいていないというお子さんが、最近ときどき見られます。
どちらかというと、２番目のイメージがわいていないケースが多いのではないか、というのが前回の内容です。
詳しくは前回のブログをお読みください。

そもそもかけ算をどう学んでいるのか

では、なぜそういう状態になってしまうのか？
これが今回のテーマです。
一番可能性が高いのは、そもそもかけ算の意味やイメージがはっきり持てていない、ということです。
わり算はかけ算を習得したあとに、その逆の操作として学習します。
わり算のベースにかけ算があり、その際に日本人は九九として覚えるわけです。
このときに、かけ算ということがしているイメージが、すでに持てていないのではないかということです。

九九は計算の答えを丸暗記しているわけです。
これ自体は計算をより早く正確にするための知恵で、決して悪いことではありません。
しかし、九九を覚える前に、かけ算がどういうことをしているのかが、はっきり理解できていないのではないか？
よく意味もわからず、計算結果だけを丸暗記しているのではないか？というのがひとつの仮説です。

意味もわからず丸暗記の状態になっていることが中学受験の算数では多いと、よくこのブログで書いています。
今回のテーマのチェックポイント①についての回もそういうお話でした。
詳しくは以下のブログをお読みください。
【中学受験でよくあるお悩み】やってもやっても伸びないのですが？②
これは、高度な中学受験算数の解法を、単純に丸暗記で乗り切ろうとするのは難しいという話です。
もちろん、さすがに計算そのものについてはそんなことはないだろう、と私も考えていたのです。
しかし、実はそうでもないのかもしれない、というのが最近の正直な実感です。

たとえば、３×５＝１５という計算は、どういう意味でしょうか？
これは、３を５個足しましょう、ということです。
それを、３＋３＋３＋３＋３＋３＝１５とやるのは面倒なので、３×５＝１５と表します。
これは、ひとつのお約束です。
しかし、九九の表には、おそらく計算がやっていることの意味やイメージは説明されていないと思います。
単に計算式と結果だけがのっていて、それを「ににんがし」「にさんがろく」と唱えて覚えるわけです。

もちろん、小学校の授業で先生はきちんと説明されていると思います。
しかし、それがしっかり理解されないまま、単に結果だけをおぼえているのではないかということです。
「６×５ってことは、６を５つ集めて足しているってことだよなー」と、考えられているのかどうか？
もしそれがないとすると、その逆のわり算を学習するときに、意味がわからなくなっても仕方がないと思います。
しかも、１５÷３＝５という計算は、３×５＝１５の逆でもあるし、５×３＝１５の逆でもあるわけです。
また同時に、１５÷５＝３という計算も、３×５＝１５の逆でもあるし、５×３＝１５の逆でもあります。
こう考えると、かけ算とわり算の関係は案外複雑であることがわかると思います。

それでも、九九を覚えてさえいればかけ算はできるわけです。
ですから、そこまで複雑なことを考えるのでなければ、なにも問題はないと思います。
しかし、中学受験算数のような難易度の高い問題になってくると、基礎的な理解不足が大きな影響を持ちます。
そういった小さな理解不足がどんどんと積み重なって、やがて算数ができなくなっていくのかなと感じます。

かけ算の順番は重要か？

１０年以上も前の話になります。
私がまだ塾の先生として駆け出しだったころ、とある有名な算数の先生の講演を聞きました。
そのときに、その先生は以下のようなことを力説されていました。

かけ算の順番をいい加減に書いているのはよくない。
３×５と、５×３は意味が違う。
３×５は３＋３＋３＋３＋３ということで、５×３は５＋５＋５ということだ。
だから、３人に５個ずつのものを配ると全部で何個？という問題文に対して、３×５と書いていたら×だ。
なぜ３×５と５×３を別々のものとして覚えているのか、そこをきちんと考えて指導したほうがいい。
ここを大事にしないと、いずれ算数も数学もできなくなる。

私の記憶では、このような内容でした。
当時の私は、まだ駆け出しだったのもあって、そこまで細かくチェックする必要があるかな？と感じました。
同じ講演を聞いていた同僚の英語の先生にも、「あれってそこまで重要？」と質問されました。
少なくとも自分はそこまで気にしていない、というのが私の返事でした。
この話は、その後もなんとなく頭の片隅にはあったのですが、そこまで重要な話と認識はしてなかったです。
しかし、最近になってこの先生の話の意味が、ようやく少しわかったような気がしています。
今回、前回のブログで書いたような状態に陥ってしまう子がいるよ、ということだったのではないかと思います。
当時の自分の未熟さと、長く現場で指導を続けている先生の知見の深さをあらためて感じます。

具体的なものと数を結びつける

では、こういった状態に陥らないためには、どうしたらいいでしょうか？
私が最近よく感じるのは、小学校１年生や２年生のころの算数セットはやはり大切なのだなということです。
数のカードやおはじき、さいころやブロック、時計の模型などが入っているあれです。
具体的なものと数を対応させて、手や体を動かして「ああでもない、こうでもない」と考えてみる。
そういった経験をしっかり持つことが、数や計算のイメージを正しく持つことにつながります。
そもそも数は抽象的な概念なので、それを具体化してイメージできているかは、非常に大切です。
低学年のお子さんについては、こういったことを大切に毎日の算数の学習をしましょう。
かけ算を学習するときも、「３このおはじきを５組集めるのだから…」ともののイメージと結びつけて学びましょう。
月並みな結論に聞こえるかもしれませんが、学校の教科書や教材はやはりよくできているということです。

では、すでに中学受験の勉強を始めている、４年生や５年生の場合はどうしたらいいでしょうか？
すでに基礎的な計算は学習済みの学年ですから、いまさら算数セットからやり直すわけにもいきません。
しかも、表面的には計算自体はできているので、本当にわかっていないのかがぱっと見はわからないのです。
こうなってくると、どう理解しているのか本人に聞いてみて、わかっていないなら一から教え直すしかないです。
算数は理解不足なことがわかったら、とにかくそこまでさかのぼって理解し直すことが鉄則です。

問題は、それがご家庭ではチェックできない、チェックはできても教え直せない、という場合です。
これについては、毎度毎度の結論で恐縮ですが、できればプロの先生に頼ってください。
どういうことの理解不足が、どういうことのできなさにつながっていくのか、それをわかっているのがプロです。
ご家庭から見れば「まさかそんなことが…」というようなことも、経験上わかっているものです。
理解不足な点がないか、そのチェックだけでもプロの先生にお願いするのが良いです。

今回は以上です。
次回は、このテーマの総まとめ的な内容になります。
８回にわたって書いてきた内容を総括して、新しいテーマに進みたいと思います。
では、また次回お会いしましょう。